728x90
최단경로 찾기 문제
우선순위 큐를 이용한다.
Swift에서 우선순위큐는 직접 만들어야 한다.
min Heap 으로 만들면 최적이지만 구현의 편리함을 위해 이번 코드에서는
배열로 sort 해서 removeLast로 min값을 찾아 처리한다.
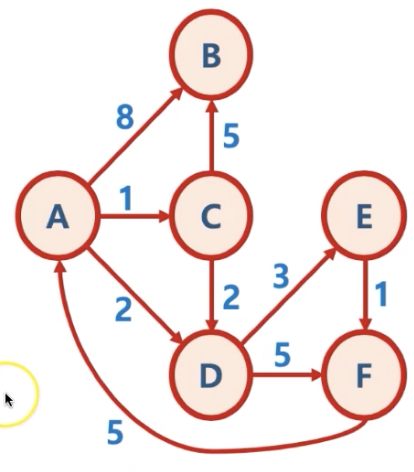
//dijkstra
var graph : [String: [(String,Int)]] = [:]
graph.updateValue([("B",8),("C",1),("D",2)], forKey: "A")
graph.updateValue([], forKey: "B")
graph.updateValue([("B",5),("D",2)], forKey: "C")
graph.updateValue([("E",3),("F",5)], forKey: "D")
graph.updateValue([("F",1)], forKey: "E")
graph.updateValue([("A",5)], forKey: "F")
for items in graph {
for item in items.value {
print("\(items.key) -> \(item.0) : \(item.1)")
}
}
print(dijkstra(graph,"A"))
func dijkstra(_ graph : [String: [(String,Int)]], _ start : String) -> [String:Int] {
//최단 거리 배열 INF로 초기화
var distances : [String:Int] = [:]
for item in graph {
distances.updateValue(Int.max, forKey: item.key)
}
//본인 출발 도착 0
distances[start] = 0
//우선순위 큐 (일단 배열로 구현 key는 거리)
var pq : [(Int,String)] = [(distances[start]!,start)]
while pq.count != 0 {
print(pq)
pq.sort{ $0 > $1 }
let dequeued = pq.removeLast()
let currentDistance = dequeued.0
let currentNode = dequeued.1
if distances[currentNode]! < currentDistance {
continue
}
for (adjacent,weight) in graph[currentNode]! {
print(pq)
let distance = currentDistance + weight
if distance < distances[adjacent]! {
distances[adjacent] = distance
pq.append((distance,adjacent))
}
}
}
return distances
}
output
A -> B : 8
A -> C : 1
A -> D : 2
D -> E : 3
D -> F : 5
C -> B : 5
C -> D : 2
E -> F : 1
F -> A : 5
[(0, "A")]
[]
[(8, "B")]
[(8, "B"), (1, "C")]
[(8, "B"), (1, "C"), (2, "D")]
[(8, "B"), (2, "D")]
[(8, "B"), (2, "D"), (6, "B")]
[(8, "B"), (2, "D"), (6, "B")]
[(8, "B"), (6, "B")]
[(8, "B"), (6, "B"), (5, "E")]
[(8, "B"), (6, "B"), (5, "E"), (7, "F")]
[(8, "B"), (7, "F"), (6, "B")]
[(8, "B"), (7, "F"), (6, "B"), (6, "F")]
[(8, "B"), (7, "F"), (6, "F")]
[(8, "B"), (7, "F")]
[(8, "B"), (7, "F")]
[(8, "B")]
["D": 2, "E": 5, "A": 0, "F": 6, "C": 1, "B": 6]
Program ended with exit code: 0
시간 복잡도
- 각 노드마다 인접한 간선들을 모드 검사 : O(E)
- 우선순위 큐에 넣고 pop 하는 시간 : O(ElogE) //heap 이라고 가정하면, 위 코드는 배열 sort 하는 시간 걸림
- 최적 : O(ElogE)
728x90
'Algorithm > Study' 카테고리의 다른 글
| LinkedList (Swift) (0) | 2021.01.28 |
|---|---|
| 탐욕 알고리즘과 예제문제 (Swift) (0) | 2021.01.20 |
| Graph Swift (BFS, DFS) (0) | 2021.01.20 |
| Swift Heap (0) | 2021.01.18 |
| 이진트리 연산 (0) | 2021.01.16 |


댓글