728x90
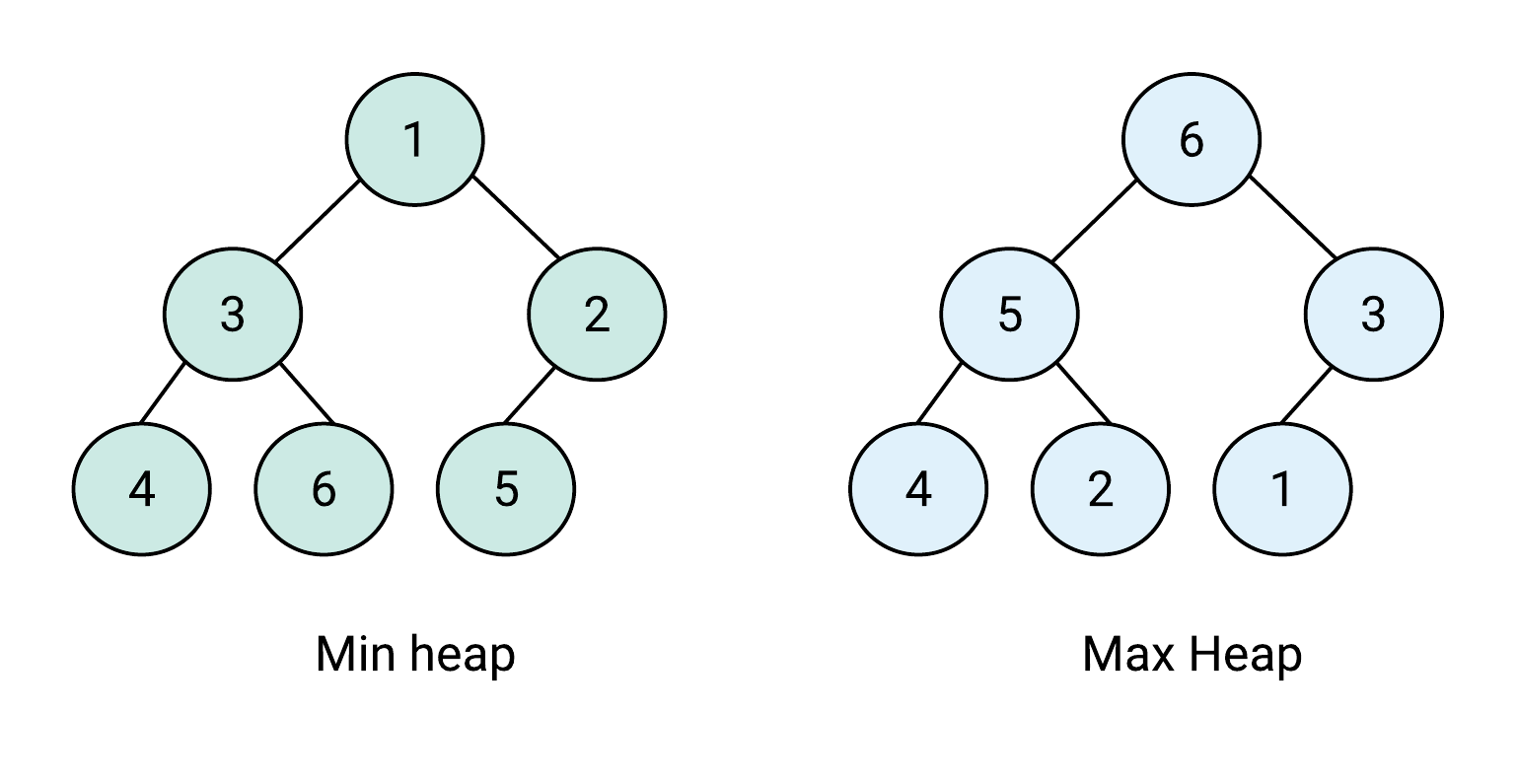
Heap
여러개의 값들 중에서 가장 큰 값이나 가장 작은 값을 빠르게 찾아내도록 만들어진 자료구조
- 완전 이진 트리 (이진 탐색 트리와 다름)
- 중복허용
- 트리 좌측부터 node 추가됨
삽입
- 완전 이진트리 만족하게 배열의 맨 마지막에 삽입
- 부모노드와 비교하며 한칸씩 올림
삭제
heap 에서는 root를 삭제함 (우선순위큐)
- root 삭제
- 제일 작은 값 (배열끝값) 을 root로 옮김
- child node 와 비교 (둘다 클 경우 둘 중 큰값과 swap)
code
import Foundation
var heap : [Int] = []
//본인 index i 일때
//parent index: i/2
//left child index: 2*i
//right child index: 2*i+1
heap.append(-1) //index start from 1
var nums = [15,10,8,5,4,20]
print(heap)
for num in nums {
add(num)
}
print(heap)
pop()
print(heap)
func pop() -> Int {
if heap.count <= 1 {
print("error no element in heap")
return -1
}
//root를 없앰
let root = heap[1]
//배열 끝 node를 root 랑 swap
heap[1] = heap.removeLast()
var poppedIndex = 1
//root를 아래로 내려가며 비교
//자식노드가 없을때, 자식노드보다 클때까지 반복
while shouldMoveDown(poppedIndex) {
let leftChild = poppedIndex*2
let rightChild = poppedIndex*2+1
//case2 자식노드 left만 있는 경우
if leftChild >= heap.count {
if heap[poppedIndex] < heap[leftChild] {
//swap
let tmp = heap[poppedIndex]
heap[poppedIndex] = heap[leftChild]
heap[leftChild] = tmp
poppedIndex = leftChild
}
}
//case3 둘다 있는 경우
else {
if heap[leftChild] > heap[rightChild] {
if heap[poppedIndex] < heap[leftChild] {
//swap
let tmp = heap[poppedIndex]
heap[poppedIndex] = heap[leftChild]
heap[leftChild] = tmp
poppedIndex = leftChild
}
}else {
if heap[poppedIndex] < heap[rightChild] {
//swap
//swap
let tmp = heap[poppedIndex]
heap[poppedIndex] = heap[rightChild]
heap[rightChild] = tmp
poppedIndex = rightChild
}
}
}
break
}
return root
}
func add(_ val : Int) {
heap.append(val)
//node 위치 찾아줘야함
var insertedIndex = heap.count-1
while shouldMoveUp(insertedIndex) {
let parentIndex = insertedIndex/2
//swap
let tmp = heap[parentIndex]
heap[parentIndex] = heap[insertedIndex]
heap[insertedIndex] = tmp
//update index
insertedIndex = parentIndex
}
}
func shouldMoveUp(_ insertedIndex : Int) -> Bool {
if insertedIndex <= 1 { //root node
return false
}
let parentIndex = insertedIndex/2
if heap[parentIndex] < heap[insertedIndex] {
return true
}else {
return false
}
}
func shouldMoveDown(_ poppedIndex: Int) -> Bool {
if poppedIndex == heap.count-1 {
return false
}
let leftChild = poppedIndex*2
let rightChild = poppedIndex*2+1
//case1 자식노드 없는 경우
if leftChild >= heap.count {
return false
}
//case2 자식노드 left만 있는 경우
else if leftChild >= heap.count {
if heap[poppedIndex] < heap[leftChild] {
//swap
return true
}else{
return false
}
}
//case3 둘다 있는 경우
else {
if heap[leftChild] > heap[rightChild] {
if heap[poppedIndex] < heap[leftChild] {
return true
}else{
return false
}
}else {
if heap[poppedIndex] < heap[rightChild] {
return true
}else{
return false
}
}
}
}output
[-1]
[-1, 20, 10, 15, 5, 4, 8]
[-1, 15, 10, 8, 5, 4]삽입, 삭제 시간복잡도
depth 를 h라 한다면 최악의 경우 root에서 leaf까지 비교해야함
O(logn)
728x90
'Algorithm > Study' 카테고리의 다른 글
| 탐욕 알고리즘과 예제문제 (Swift) (0) | 2021.01.20 |
|---|---|
| Graph Swift (BFS, DFS) (0) | 2021.01.20 |
| 이진트리 연산 (0) | 2021.01.16 |
| 이진트리 순회 (0) | 2021.01.16 |
| Swift Sorting Algorithm Note (0) | 2021.01.13 |

댓글