🎓 졸업과제 - Python3, Pycharm, Homebrew update
잠자던 졸업과제 단톡방에 조교님의 톡이 올라왔다.
우선 자바스크립트 버튼 누르면 파일 선택하고 선택된 HTML 테이블 코드가 있는 텍스트파일의 테이블을 출력하는 부분을 구현해주셔야 할 것 같습니다네 알겠습니다.
구현할 것
- 자바스크립트 버튼을 누르면 파일을 선택한다.
- 파일(HTML파일인것 같음) 에서 <Table> </Table> 만 뽑는다.
- 뽑아낸 표의 데이터를 출력한다.
1. 파이참 Community 버전을 깐다.
다운로드 PyCharm: JetBrains가 만든 전문 개발자용 Python IDE
최신 버전 다운로드: PyCharm (Windows, macOS, Linux)
www.jetbrains.com
2. 외부 라이브러리를 설치한다.
Mac 기준 Preference -> Project -> Project Interpreter
requests 설치
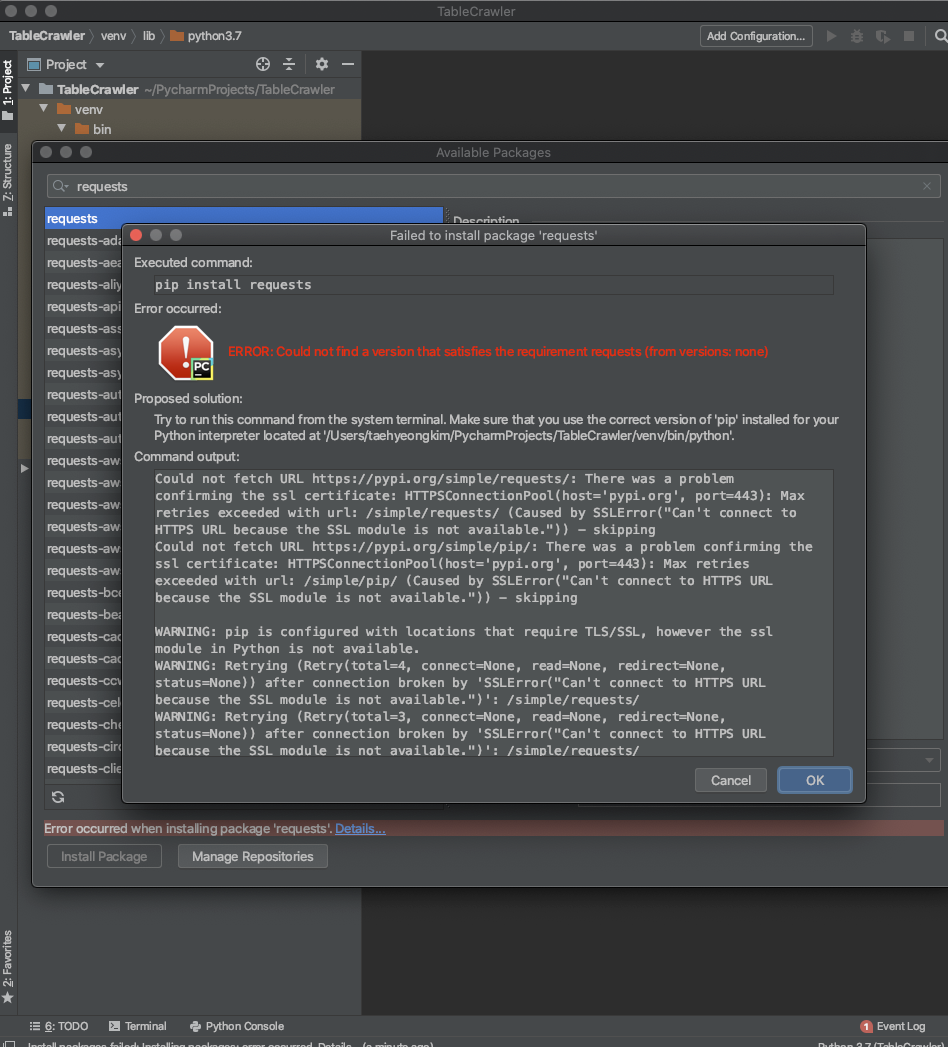
에러난다. pip 가 없단다.
homebrew 로 pip 를 깔아준다.
$ sudo easy_install pip
아 파이썬3 이라서 안되는거 같다. pip 는 깔려있다.

맥 사용자 바꾸고 난 뒤로부터 Homebrew premission denied 가 뜬다. 이참에 고쳐봐야겠다.
sudo chown -R $(whoami) /usr/local/Homebrew/
에러뜨는 디렉토리 전부 chown 으로 권한을 설정해 준다.
을마나 업데이트를 안했 homebrew update 한참 걸린다.
brew install python3아 근데 파이참에 파이썬3이라도 되있는데
하 열받네 파이썬
일단 시간이 늦어서
그냥 HomeBrew 에 파이썬 다지우고 내일 깨끗한 마음으로
처음부터 해야겠다.
Homebrew Package 지울땐
brew list
brew remove python
그냥 안자고 다시 설치 해봤다.

beautifulsoup4도 설치해준다.

아 이제 HTML 에서 데이터 뽑아보자
원주율 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 3.1415926535897932384626433832795…… 원주율(圓周率, 문화어: 원주률)은 원둘레와 지름의 비 즉, 원의 지름에 대한 둘레의 비율을 나타내는 수학 상수이다. 수학과 물��
ko.wikipedia.org
이 페이지의 HTML 코드를 가져오겠다.
import requests
req = requests.get("https://ko.wikipedia.org/wiki/%EC%9B%90%EC%A3%BC%EC%9C%A8")
raw = req.text
print(raw)
/Users/taehyeongkim/PycharmProjects/TableCrawler/venv/bin/python /Users/taehyeongkim/PycharmProjects/TableCrawler/crawler/htmlTableCrawler.py
<!DOCTYPE html>
<html class="client-nojs" lang="ko" dir="ltr">
<head>
<meta charset="UTF-8"/>
<title>원주율 - 위키백과, 우리 모두의 백과사전</title>
<script>document.documentElement.className="client-js";RLCONF={"wgBreakFrames":!1,"wgSeparatorTransformTable":["",""],"wgDigitTransformTable":["",""],"wgDefaultDateFormat":"ko","wgMonthNames":["","1월","2월","3월","4월","5월","6월","7월","8월","9월","10월","11월","12월"],"wgRequestId":"c2037141-a927-42c5-9e65-426a587c8a8d","wgCSPNonce":!1,"wgCanonicalNamespace":"","wgCanonicalSpecialPageName":!1,"wgNamespaceNumber":0,"wgPageName":"원주율","wgTitle":"원주율","wgCurRevisionId":27000186,"wgRevisionId":27000186,"wgArticleId":284,"wgIsArticle":!0,"wgIsRedirect":!1,"wgAction":"view","wgUserName":null,"wgUserGroups":["*"],"wgCategories":["CS1 관리 - 추가 문구","CS1 - 영어 인용 (en)","깨진 링크를 가지고 있는 문서","좋은 글","문화어 표기를 포함한 문서","GND 식별자를 포함한 위키백과 문서","LCCN 식별자를 포함한 위키백과 문서","NDL 식별자를 포함한 위키백과 문서","원주율","비 (수학)",
"수학 상수","초월수","무리수","복소해석학"],"wgPageContentLanguage":"ko","wgPageContentModel":"wikitext","wgRelevantPageName":"원주율","wgRelevantArticleId":284,"wgIsProbablyEditable":!0,"wgRelevantPageIsProbablyEditable":!0,"wgRestrictionEdit":[],"wgRestrictionMove":[],"wgMediaViewerOnClick":!0,"wgMediaViewerEnabledByDefault":!0,"wgPopupsReferencePreviews":!1,"wgPopupsConflictsWithNavPopupGadget":!1,"wgVisualEditor":{"pageLanguageCode":"ko","pageLanguageDir":"ltr","pageVariantFallbacks":"ko"},"wgMFDisplayWikibaseDescriptions":{"search":!0,"nearby":!0,"watchlist":!0,"tagline":!0},"wgWMESchemaEditAttemptStepOversample":!1,"wgULSCurrentAutonym":"한국어","wgNoticeProject":"wikipedia","wgCentralAuthMobileDomain":!1,"wgEditSubmitButtonLabelPublish":!0,"wgULSPosition":"interlanguage","wgWikibaseItemId":"Q167","wgGENewcomerTasksGuidanceEnabled":!0};RLSTATE={"ext.globalCssJs.user.styles":"ready","site.styles":"ready","noscript":"ready",
"user.styles":"ready","ext.globalCssJs.user":"ready","user":"ready","user.options":"loading","ext.cite.styles":"ready","ext.math.styles":"ready","skins.vector.styles.legacy":"ready","jquery.makeCollapsible.styles":"ready","mediawiki.toc.styles":"ready","ext.visualEditor.desktopArticleTarget.noscript":"ready","ext.uls.interlanguage":"ready","ext.wikimediaBadges":"ready","wikibase.client.init":"ready"};RLPAGEMODULES=["ext.cite.ux-enhancements","ext.math.scripts","site","mediawiki.page.startup","mediawiki.page.ready","jquery.makeCollapsible","mediawiki.toc","skins.vector.legacy.js","ext.gadget.directcommons","ext.gadget.ReferenceTooltips","ext.gadget.refToolbar","ext.gadget.siteNotice","ext.gadget.CollapsibleSidebar","ext.gadget.scrollUpButton","ext.centralauth.centralautologin","mmv.head","mmv.bootstrap.autostart","ext.popups","ext.visualEditor.desktopArticleTarget.init","ext.visualEditor.targetLoader","ext.eventLogging","ext.wikimediaEvents","ext.navigationTiming","ext.uls.compactlinks"
,"ext.uls.interface","ext.cx.eventlogging.campaigns","ext.growthExperiments.SuggestedEditSession","ext.centralNotice.geoIP","ext.centralNotice.startUp"];</script>
<script>(RLQ=window.RLQ||[]).push(function(){mw.loader.implement("user.options@1hzgi",function($,jQuery,require,module){/*@nomin*/mw.user.tokens.set({"patrolToken":"+\\","watchToken":"+\\","csrfToken":"+\\"});mw.user.options.set({"variant":"ko"});
});});</script>
<link rel="stylesheet" href="/w/load.php?lang=ko&modules=ext.cite.styles%7Cext.math.styles%7Cext.uls.interlanguage%7Cext.visualEditor.desktopArticleTarget.noscript%7Cext.wikimediaBadges%7Cjquery.makeCollapsible.styles%7Cmediawiki.toc.styles%7Cskins.vector.styles.legacy%7Cwikibase.client.init&only=styles&skin=vector"/>
<script async="" src="/w/load.php?lang=ko&modules=startup&only=scripts&raw=1&skin=vector"></script>
<meta name="ResourceLoaderDynamicStyles" content=""/>
<link rel="stylesheet" href="/w/load.php?lang=ko&modules=site.styles&only=styles&skin=vector"/>
<meta name="generator" content="MediaWiki 1.35.0-wmf.40"/>
<meta name="referrer" content="origin"/>
<meta name="referrer" content="origin-when-crossorigin"/>
<meta name="referrer" content="origin-when-cross-origin"/>
<meta property="og:image" content="https://upload.wikimedia.org/wikipedia/commons/thumb/2/2e/Pi-symbol.svg/1200px-Pi-symbol.svg.png"/>
<link rel="alternate" media="only screen and (max-width: 720px)" href="//ko.m.wikipedia.org/wiki/%EC%9B%90%EC%A3%BC%EC%9C%A8"/>
<link rel="alternate" type="application/x-wiki" title="편집" href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8&action=edit"/>
<link rel="edit" title="편집" href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8&action=edit"/>
<link rel="apple-touch-icon" href="/static/apple-touch/wikipedia.png"/>
<link rel="shortcut icon" href="/static/favicon/wikipedia.ico"/>
<link rel="search" type="application/opensearchdescription+xml" href="/w/opensearch_desc.php" title="위키백과 (ko)"/>
<link rel="EditURI" type="application/rsd+xml" href="//ko.wikipedia.org/w/api.php?action=rsd"/>
<link rel="license" href="//creativecommons.org/licenses/by-sa/3.0/"/>
<link rel="canonical" href="https://ko.wikipedia.org/wiki/%EC%9B%90%EC%A3%BC%EC%9C%A8"/>
<link rel="dns-prefetch" href="//login.wikimedia.org"/>
<link rel="dns-prefetch" href="//meta.wikimedia.org" />
<!--[if lt IE 9]><script src="/w/resources/lib/html5shiv/html5shiv.js"></script><![endif]-->
</head>
<body class="mediawiki ltr sitedir-ltr mw-hide-empty-elt ns-0 ns-subject mw-editable page-원주율 rootpage-원주율 skin-vector action-view skin-vector-legacy minerva--history-page-action-enabled">
<div id="mw-page-base" class="noprint"></div>
<div id="mw-head-base" class="noprint"></div>
<div id="content" class="mw-body" role="main">
<a id="top"></a>
<div id="siteNotice" class="mw-body-content"><!-- CentralNotice --></div>
<div class="mw-indicators mw-body-content">
<div id="mw-indicator-featured-star" class="mw-indicator"><a href="/wiki/%EC%9C%84%ED%82%A4%EB%B0%B1%EA%B3%BC:%EC%A2%8B%EC%9D%80_%EA%B8%80" title="이 글은 좋은 글로 선정되었습니다."><img alt="이 글은 좋은 글로 선정되었습니다." src="//upload.wikimedia.org/wikipedia/commons/thumb/a/ab/Simple_GA.svg/20px-Simple_GA.svg.png" decoding="async" width="20" height="19" srcset="//upload.wikimedia.org/wikipedia/commons/thumb/a/ab/Simple_GA.svg/30px-Simple_GA.svg.png 1.5x, //upload.wikimedia.org/wikipedia/commons/thumb/a/ab/Simple_GA.svg/40px-Simple_GA.svg.png 2x" data-file-width="91" data-file-height="87" /></a></div>
</div>
<h1 id="firstHeading" class="firstHeading" lang="ko">원주율</h1>
<div id="bodyContent" class="mw-body-content">
<div id="siteSub" class="noprint">위키백과, 우리 모두의 백과사전.</div>
<div id="contentSub"></div>
<div id="jump-to-nav"></div>
<a class="mw-jump-link" href="#mw-head">둘러보기로 가기</a>
<a class="mw-jump-link" href="#searchInput">검색하러 가기</a>
<div id="mw-content-text" lang="ko" dir="ltr" class="mw-content-ltr"><div class="mw-parser-output"><p class="mw-empty-elt">
</p>
<table class="toccolours" style="float:right; border: 2px solid #eeeeee; margin: 0 0 1em 1em; width:250px;">
<tbody><tr>
<td style="text-align:center;"><a href="/wiki/%ED%8C%8C%EC%9D%BC:Pi-symbol.svg" class="image"><img alt="Pi-symbol.svg" src="//upload.wikimedia.org/wikipedia/commons/thumb/2/2e/Pi-symbol.svg/150px-Pi-symbol.svg.png" decoding="async" width="150" height="145" srcset="//upload.wikimedia.org/wikipedia/commons/thumb/2/2e/Pi-symbol.svg/225px-Pi-symbol.svg.png 1.5x, //upload.wikimedia.org/wikipedia/commons/thumb/2/2e/Pi-symbol.svg/300px-Pi-symbol.svg.png 2x" data-file-width="588" data-file-height="569" /></a><br />3.1415926535897932384626433832795……
</td></tr></tbody></table>
<table class="vertical-navbox nowraplinks" style="float:right;clear:right;width:200px;margin:0 0 1.0em 1.0em;background:#f9f9f9;border:1px solid #aaa;padding:0.2em;border-spacing:0.4em 0;text-align:center;line-height:1.4em;font-size:88%"><tbody><tr><th style="padding:0.2em 0.4em 0.2em;font-size:145%;line-height:1.2em;font-size:130%;"><a class="mw-selflink selflink">원주율</a></th></tr><tr><td style="padding:0.2em 0 0.4em"><a href="/wiki/%ED%8C%8C%EC%9D%BC:Pi-unrolled-720.gif" class="image"><img alt="Pi-unrolled-720.gif" src="//upload.wikimedia.org/wikipedia/commons/thumb/2/2a/Pi-unrolled-720.gif/200px-Pi-unrolled-720.gif" decoding="async" width="200" height="63" srcset="//upload.wikimedia.org/wikipedia/commons/thumb/2/2a/Pi-unrolled-720.gif/300px-Pi-unrolled-720.gif 1.5x, //upload.wikimedia.org/wikipedia/commons/thumb/2/2a/Pi-unrolled-720.gif/400px-Pi-unrolled-720.gif 2x" data-file-width="720" data-file-height="228" /></a></td></tr><tr><th style="padding:0.1em;border-top:#aaa 1px solid;">
이용</th></tr><tr><td style="padding:0 0.1em 0.4em;hlist">
<a href="/w/index.php?title=%EC%9B%90%EB%84%93%EC%9D%B4&action=edit&redlink=1" class="new" title="원넓이 (없는 문서)">원넓이</a>  <span style="font-weight:bold;">·</span> <a href="/wiki/%EC%9B%90%EB%91%98%EB%A0%88" title="원둘레">원둘레</a>  <span style="font-weight:bold;">·</span> <a href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8%EC%9D%84_%ED%8F%AC%ED%95%A8%ED%95%98%EB%8A%94_%EC%88%98%EC%8B%9D_%EB%AA%A9%EB%A1%9D&action=edit&redlink=1" class="new" title="원주율을 포함하는 수식 목록 (없는 문서)">기타 이용</a></td>
</tr><tr><th style="padding:0.1em;border-top:#aaa 1px solid;">
특성</th></tr><tr><td style="padding:0 0.1em 0.4em;hlist">
<a href="/wiki/%EC%9B%90%EC%A3%BC%EC%9C%A8%EC%9D%98_%EB%AC%B4%EB%A6%AC%EC%84%B1_%EC%A6%9D%EB%AA%85" title="원주율의 무리성 증명">무리수</a>  <span style="font-weight:bold;">·</span> <a href="/w/index.php?title=%EB%A6%AC%EB%A7%8C-%EB%B0%94%EC%9D%B4%EC%96%B4%EC%8A%88%ED%8A%B8%EB%9D%BC%EC%B8%A0_%EC%A0%95%EB%A6%AC&action=edit&redlink=1" class="new" title="리만-바이어슈트라츠 정리 (없는 문서)">초월수</a></td>
</tr><tr><th style="padding:0.1em;border-top:#aaa 1px solid;">
유용성</th></tr><tr><td style="padding:0 0.1em 0.4em;hlist">
<a href="/w/index.php?title=22/7%EC%9D%B4_%EC%9B%90%EC%A3%BC%EC%9C%A8%EB%B3%B4%EB%8B%A4_%ED%81%AC%EB%8B%A4%EB%8A%94_%EC%A6%9D%EB%AA%85&action=edit&redlink=1" class="new" title="22/7이 원주율보다 크다는 증명 (없는 문서)">22/7보다 작음증명</a>  <span style="font-weight:bold;">·</span> <a href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8%EC%9D%98_%EA%B7%BC%EC%82%AC%EA%B0%92&action=edit&redlink=1" class="new" title="원주율의 근사값 (없는 문서)">근사값</a>  <span style="font-weight:bold;">·</span> <a href="/w/index.php?title=%ED%8C%8C%EC%9D%B4%EC%98%AC%EB%A1%9C%EC%A7%80&action=edit&redlink=1" class="new" title="파이올로지 (없는 문서)">값 암기</a></td>
</tr><tr><th style="padding:0.1em;border-top:#aaa 1px solid;">
관련 인물</th></tr><tr><td style="padding:0 0.1em 0.4em;hlist">
<p><a href="/w/index.php?title=%EC%95%84%EB%A5%B4%ED%82%A4%EB%A9%94%EB%8D%B0%EC%8A%A4_%EC%86%8C%EA%B1%B0%EB%B2%95&action=edit&redlink=1" class="new" title="아르키메데스 소거법 (없는 문서)">아르키메데스</a>  <span style="font-weight:bold;">·</span> <a href="/w/index.php?title=%EC%9C%A0%ED%9C%98%EC%9D%98_%EC%9B%90%EC%A3%BC%EC%9C%A8_%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98&action=edit&redlink=1" class="new" title="유휘의 원주율 알고리즘 (없는 문서)">유휘</a>  <span style="font-weight:bold;">·</span> <a href="/wiki/%EC%A1%B0%EC%B6%A9%EC%A7%80" title="조충지">조충지</a><br />
<a href="/w/index.php?title=%EC%82%B0%EA%B0%80%EB%A7%88%EA%B7%B8%EB%9D%BC%EB%A7%88%EC%9D%98_%EB%A7%88%EB%93%9C%ED%95%98%EB%B0%94&action=edit&redlink=1" class="new" title="산가마그라마의 마드하바 (없는 문서)">산가마그라마의 마드하바</a>  <span style="font-weight:bold;">·</span> <a href="/w/index.php?title=%EC%9C%8C%EB%A6%AC%EC%97%84_%EC%A1%B0%EC%9D%B4%EC%8A%A4_(%EC%88%98%ED%95%99%EC%9E%90)&action=edit&redlink=1" class="new" title="윌리엄 조이스 (수학자) (없는 문서)">윌리엄 조이스</a>  <span style="font-weight:bold;">·</span> <a href="/w/index.php?title=%EC%A1%B4_%EB%A7%88%EC%B9%9C&action=edit&redlink=1" class="new" title="존 마친 (없는 문서)">존 마친</a><br />
</p>
<a href="/w/index.php?title=%EC%A1%B4_%EB%A0%8C%EC%B9%98&action=edit&redlink=1" class="new" title="존 렌치 (없는 문서)">존 렌치</a>  <span style="font-weight:bold;">·</span> <a href="/wiki/%EB%A4%BC%EB%8F%8C%ED%94%84_%ED%8C%90_%EC%BE%B0%EB%9F%B0" title="뤼돌프 판 쾰런">뤼돌프 판 쾰런</a>  <span style="font-weight:bold;">·</span> <a href="/wiki/%EC%95%84%EB%A6%AC%EC%95%84%EB%B0%94%ED%83%80" title="아리아바타">아리아바타</a></td>
</tr><tr><th style="padding:0.1em;border-top:#aaa 1px solid;">
역사</th></tr><tr><td style="padding:0 0.1em 0.4em;hlist">
<a href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8_%EA%B0%92_%EA%B3%84%EC%82%B0%EC%9D%98_%EC%97%B0%EB%8C%80%EA%B8%B0&action=edit&redlink=1" class="new" title="원주율 값 계산의 연대기 (없는 문서)">연대기</a>  <span style="font-weight:bold;">·</span> <a href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8%EC%9D%98_%EC%97%AD%EC%82%AC&action=edit&redlink=1" class="new" title="원주율의 역사 (없는 문서)">원주율의 역사</a></td>
</tr><tr><th style="padding:0.1em;border-top:#aaa 1px solid;">
원주율과 문화</th></tr><tr><td style="padding:0 0.1em 0.4em;hlist">
<a href="/w/index.php?title=%EC%9D%B8%EB%94%94%EC%95%A0%EB%82%98_%EC%9B%90%EC%A3%BC%EC%9C%A8%EA%B0%92_%EB%B2%95&action=edit&redlink=1" class="new" title="인디애나 원주율값 법 (없는 문서)">입법</a>  <span style="font-weight:bold;">·</span> <a href="/wiki/%ED%8C%8C%EC%9D%B4%EC%9D%98_%EB%82%A0" title="파이의 날">파이의 날</a></td>
</tr><tr><th style="padding:0.1em;border-top:#aaa 1px solid;">
기타</th></tr><tr><td style="padding:0 0.1em 0.4em;hlist">
<a href="/wiki/%EC%9B%90%EC%A0%81%EB%AC%B8%EC%A0%9C" title="원적문제">원적문제</a>  <span style="font-weight:bold;">·</span> <a href="/wiki/%EB%B0%94%EC%A0%A4_%EB%AC%B8%EC%A0%9C" title="바젤 문제">바젤 문제</a>  <span style="font-weight:bold;">·</span> <a href="/wiki/%ED%8C%8C%EC%9D%B8%EB%A7%8C_%ED%8F%AC%EC%9D%B8%ED%8A%B8" title="파인만 포인트">파인만 포인트</a>  <span style="font-weight:bold;">·</span> <a href="/wiki/%EB%B6%84%EB%A5%98:%EC%9B%90%EC%A3%BC%EC%9C%A8" title="분류:원주율">기타 문서..</a></td>
</tr><tr><td style="text-align:right;font-size:115%"><div class="plainlinks hlist navbar mini"><ul><li class="nv-view"><a href="/wiki/%ED%8B%80:%EC%9B%90%EC%A3%BC%EC%9C%A8" title="틀:원주율"><abbr title="이 틀을 보기">v</abbr></a></li><li class="nv-talk"><a href="/wiki/%ED%8B%80%ED%86%A0%EB%A1%A0:%EC%9B%90%EC%A3%BC%EC%9C%A8" title="틀토론:원주율"><abbr title="이 틀에 대한 토론">t</abbr></a></li><li class="nv-edit"><a class="external text" href="https://ko.wikipedia.org/w/index.php?title=%ED%8B%80:%EC%9B%90%EC%A3%BC%EC%9C%A8&action=edit"><abbr title="이 틀을 편집하기">e</abbr></a></li></ul></div></td></tr></tbody></table>
<p><b>원주율</b>(圓周率, <span style="font-size: smaller;"><a href="/wiki/%EB%AC%B8%ED%99%94%EC%96%B4" title="문화어">문화어</a>:</span> 원주률)은 <a href="/wiki/%EC%9B%90%EB%91%98%EB%A0%88" title="원둘레">원둘레</a>와 지름의 비 즉, <a href="/wiki/%EC%9B%90_(%EA%B8%B0%ED%95%98%ED%95%99)" title="원 (기하학)">원</a>의 <a href="/wiki/%EC%A7%80%EB%A6%84" title="지름">지름</a>에 대한 <a href="/wiki/%EB%91%98%EB%A0%88" title="둘레">둘레</a>의 <a href="/wiki/%EB%B9%84%EC%9C%A8" class="mw-redirect" title="비율">비율</a>을 나타내는 <a href="/wiki/%EC%88%98%ED%95%99_%EC%83%81%EC%88%98" title="수학 상수">수학 상수</a>이다. <a href="/wiki/%EC%88%98%ED%95%99" title="수학">수학</a>과 <a href="/wiki/%EB%AC%BC%EB%A6%AC%ED%95%99" title="물리학">물리학</a>의 여러 분야에 두루 쓰인다. <a href="/wiki/%EA%B7%B8%EB%A6%AC%EC%8A%A4_%EB%AC%B8%EC%9E%90" title="그리스 문자">그리스 문자</a> <a href="/wiki/%CE%A0" title="Π">π</a>로 표기하고, <b>파이</b>(π)라고 읽는다.<sup id="cite_ref-1" class="reference"><a href="#cite_note-1">[1]</a></sup> 원주율은 수학에서 다루는 가장 중요한 상수 가운데 하나이다.<sup id="cite_ref-2" class="reference"><a href="#cite_note-2">[2]</a></sup> <a href="/wiki/%EB%AC%B4%EB%A6%AC%EC%88%98" title="무리수">무리수</a>인 동시에 <a href="/wiki/%EC%B4%88%EC%9B%94%EC%88%98" title="초월수">초월수</a>이다. <a href="/wiki/%EC%95%84%EB%A5%B4%ED%82%A4%EB%A9%94%EB%8D%B0%EC%8A%A4" title="아르키메데스">아르키메데스</a>의 계산이 널리 알려져 있어 <b>아르키메데스 상수</b>라고 부르기도 하며, 독일에서는 1600년대 <a href="/wiki/%EB%A4%BC%EB%8F%8C%ED%94%84_%ED%8C%90_%EC%BE%B0%EB%9F%B0" title="뤼돌프 판 쾰런">뤼돌프 판 쾰런</a>이 소수점 이하 35자리까지 원주율을 계산한 이후 <b>뤼돌프 수</b>라고 부르기도 한다.<sup id="cite_ref-사이언스타임즈_3-0" class="reference"><a href="#cite_note-사이언스타임즈-3">[3]</a></sup> 원주율의 값은 3.141592653589793238462643383279502884197169399375105820974944...로, 순환하지 않는 무한소수이기 때문에 근삿값으로 3.14를 사용하거나 기호 <a href="/wiki/%CE%A0" title="Π">π</a>로 사용한다.
</p>
<div id="toc" class="toc" role="navigation" aria-labelledby="mw-toc-heading"><input type="checkbox" role="button" id="toctogglecheckbox" class="toctogglecheckbox" style="display:none" /><div class="toctitle" lang="ko" dir="ltr"><h2 id="mw-toc-heading">목차</h2><span class="toctogglespan"><label class="toctogglelabel" for="toctogglecheckbox"></label></span></div>
<ul>
<li class="toclevel-1 tocsection-1"><a href="#개요"><span class="tocnumber">1</span> <span class="toctext">개요</span></a></li>
<li class="toclevel-1 tocsection-2"><a href="#역사"><span class="tocnumber">2</span> <span class="toctext">역사</span></a>
<ul>
<li class="toclevel-2 tocsection-3"><a href="#고대"><span class="tocnumber">2.1</span> <span class="toctext">고대</span></a></li>
<li class="toclevel-2 tocsection-4"><a href="#컴퓨터를_통한_원주율_계산"><span class="tocnumber">2.2</span> <span class="toctext">컴퓨터를 통한 원주율 계산</span></a></li>
</ul>
</li>
<li class="toclevel-1 tocsection-5"><a href="#원주율의_값"><span class="tocnumber">3</span> <span class="toctext">원주율의 값</span></a></li>
<li class="toclevel-1 tocsection-6"><a href="#수학적_특성"><span class="tocnumber">4</span> <span class="toctext">수학적 특성</span></a>
<ul>
<li class="toclevel-2 tocsection-7"><a href="#무리수"><span class="tocnumber">4.1</span> <span class="toctext">무리수</span></a></li>
<li class="toclevel-2 tocsection-8"><a href="#초월수"><span class="tocnumber">4.2</span> <span class="toctext">초월수</span></a></li>
<li class="toclevel-2 tocsection-9"><a href="#수열"><span class="tocnumber">4.3</span> <span class="toctext">수열</span></a></li>
</ul>
</li>
<li class="toclevel-1 tocsection-10"><a href="#계산식"><span class="tocnumber">5</span> <span class="toctext">계산식</span></a></li>
<li class="toclevel-1 tocsection-11"><a href="#적용"><span class="tocnumber">6</span> <span class="toctext">적용</span></a>
<ul>
<li class="toclevel-2 tocsection-12"><a href="#기하학"><span class="tocnumber">6.1</span> <span class="toctext">기하학</span></a></li>
<li class="toclevel-2 tocsection-13"><a href="#바젤_문제"><span class="tocnumber">6.2</span> <span class="toctext">바젤 문제</span></a></li>
<li class="toclevel-2 tocsection-14"><a href="#복소수_계산"><span class="tocnumber">6.3</span> <span class="toctext">복소수 계산</span></a></li>
<li class="toclevel-2 tocsection-15"><a href="#확률과_통계"><span class="tocnumber">6.4</span> <span class="toctext">확률과 통계</span></a></li>
<li class="toclevel-2 tocsection-16"><a href="#물리학"><span class="tocnumber">6.5</span> <span class="toctext">물리학</span></a></li>
</ul>
</li>
<li class="toclevel-1 tocsection-17"><a href="#같이_보기"><span class="tocnumber">7</span> <span class="toctext">같이 보기</span></a></li>
<li class="toclevel-1 tocsection-18"><a href="#주해"><span class="tocnumber">8</span> <span class="toctext">주해</span></a></li>
<li class="toclevel-1 tocsection-19"><a href="#참고"><span class="tocnumber">9</span> <span class="toctext">참고</span></a></li>
<li class="toclevel-1 tocsection-20"><a href="#외부_링크"><span class="tocnumber">10</span> <span class="toctext">외부 링크</span></a></li>
</ul>
</div>
<h2><span id=".EA.B0.9C.EC.9A.94"></span><span class="mw-headline" id="개요">개요</span><span class="mw-editsection"><span class="mw-editsection-bracket">[</span><a href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8&action=edit&section=1" title="부분 편집: 개요">편집</a><span class="mw-editsection-bracket">]</span></span></h2>
<div class="thumb tleft"><div class="thumbinner" style="width:402px;"><a href="/wiki/%ED%8C%8C%EC%9D%BC:Pi-unrolled-720.gif" class="image"><img alt="" src="//upload.wikimedia.org/wikipedia/commons/thumb/2/2a/Pi-unrolled-720.gif/400px-Pi-unrolled-720.gif" decoding="async" width="400" height="127" class="thumbimage" srcset="//upload.wikimedia.org/wikipedia/commons/thumb/2/2a/Pi-unrolled-720.gif/600px-Pi-unrolled-720.gif 1.5x, //upload.wikimedia.org/wikipedia/commons/2/2a/Pi-unrolled-720.gif 2x" data-file-width="720" data-file-height="228" /></a> <div class="thumbcaption"><div class="magnify"><a href="/wiki/%ED%8C%8C%EC%9D%BC:Pi-unrolled-720.gif" class="internal" title="실제 크기로"></a></div>원의 지름이 1일 때, 원주는 π이다.</div></div></div>
<p><a href="/wiki/%EC%9C%A0%ED%81%B4%EB%A6%AC%EB%93%9C_%EA%B8%B0%ED%95%98%ED%95%99" title="유클리드 기하학">유클리드 평면</a>에서 <a href="/wiki/%EC%9B%90_(%EA%B8%B0%ED%95%98%ED%95%99)" title="원 (기하학)">원</a>은 크기와 관계없이 언제나 <a href="/wiki/%EB%8B%AE%EC%9D%8C_(%EA%B8%B0%ED%95%98%ED%95%99)" title="닮음 (기하학)">닮은 도형</a>이다. 따라서 원의 <a href="/wiki/%EC%A7%80%EB%A6%84" title="지름">지름</a>에 대한 <a href="/wiki/%EB%91%98%EB%A0%88" title="둘레">둘레</a>의 <a href="/wiki/%EB%B9%84_(%EC%88%98%ED%95%99)" title="비 (수학)">비</a>는 언제나 일정하며, 이를 원주율이라 한다. 즉, 원의 지름을 d, 둘레를 C라 하면 원주율 π는 다음의 식으로 나타낼 수 있다.<sup id="cite_ref-4" class="reference"><a href="#cite_note-4">[4]</a></sup>
</p>
<dl><dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \pi ={\frac {C}{d}}}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>π<!-- π --></mi>
<mo>=</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mi>C</mi>
<mi>d</mi>
</mfrac>
</mrow>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle \pi ={\frac {C}{d}}}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/d3ffc6970dda2e60597854f14e2ac1e13a25a5cf" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -2.005ex; width:7.033ex; height:5.509ex;" alt="\pi ={\frac {C}{d}}"/></span></dd></dl>
<p>원주율을 나타내는 기호 π는 1706년 영국의 수학자 <a href="/wiki/%EC%9C%8C%EB%A6%AC%EC%97%84_%EC%A1%B4%EC%8A%A4" class="mw-disambig" title="윌리엄 존스">윌리엄 존스</a>가 최초로 사용했다. 이것은 둘레를 뜻하는 <a href="/wiki/%EA%B3%A0%EB%8C%80_%EA%B7%B8%EB%A6%AC%EC%8A%A4%EC%96%B4" title="고대 그리스어">고대 그리스어</a> "페리페레스"(περιφηρής) 또는 "페리메트론"(περίμετρον)의 첫 글자를 딴 것이다.<sup id="cite_ref-5" class="reference"><a href="#cite_note-5">[5]</a></sup> 윌리엄 존스는 “특정 도형의 길이나 넓이를 구하는 계산에 매우 유용한 방법이 여러 가지 있다. 원을 예로 들면 지름이 1인 원의 둘레를 약 3.14159…= π로 표기하는 것이다.”라고 기호 π의 사용을 제안하였다.<sup id="cite_ref-6" class="reference"><a href="#cite_note-6">[6]</a></sup>
</p><p>원주율은 소수점 아래 어느 자리에서도 끝나지 않고, <a href="/wiki/%EC%88%9C%ED%99%98%EB%A7%88%EB%94%94" class="mw-redirect" title="순환마디">순환마디</a>도 없이 무한히 계속되는 <a href="/wiki/%EB%AC%B4%EB%A6%AC%EC%88%98" title="무리수">비</a><a href="/wiki/%EC%88%9C%ED%99%98%EC%86%8C%EC%88%98" title="순환소수">순환소수</a>이다. 원주율이 <a href="/wiki/%EB%AC%B4%EB%A6%AC%EC%88%98" title="무리수">무리수</a>라는 것은 <a href="/wiki/1761%EB%85%84" title="1761년">1761년</a> <a href="/w/index.php?title=%EC%9A%94%ED%95%9C_%ED%95%98%EC%9D%B8%EB%A6%AC%ED%9E%88_%EB%9E%8C%EB%B2%A0%EB%A5%B4%ED%8A%B8&action=edit&redlink=1" class="new" title="요한 하인리히 람베르트 (없는 문서)">요한 하인리히 람베르트</a>가 증명했다. 원주율의 소수점 이하에서 나타나는 수열은 무작위 <a href="/wiki/%ED%91%9C%EC%A7%91" title="표집">표집</a>을 통해 만드는 난수표와 성질이 같다.<sup id="cite_ref-sciencedaily.com_7-0" class="reference"><a href="#cite_note-sciencedaily.com-7">[7]</a></sup> 원주율은 <a href="/wiki/%EC%8B%AD%EC%A7%84%EB%B2%95" title="십진법">십진법</a>으로는 값을 정확하게 표기할 수 없기 때문에 실제 계산에서는 근삿값을 이용한다.
</p><p><br clear="left" />
</p>
<div class="thumb tleft"><div class="thumbinner" style="width:174px;"><a href="/wiki/%ED%8C%8C%EC%9D%BC:Circle_Area.svg" class="image"><img alt="" src="//upload.wikimedia.org/wikipedia/commons/thumb/c/ce/Circle_Area.svg/172px-Circle_Area.svg.png" decoding="async" width="172" height="172" class="thumbimage" srcset="//upload.wikimedia.org/wikipedia/commons/thumb/c/ce/Circle_Area.svg/258px-Circle_Area.svg.png 1.5x, //upload.wikimedia.org/wikipedia/commons/thumb/c/ce/Circle_Area.svg/344px-Circle_Area.svg.png 2x" data-file-width="265" data-file-height="265" /></a> <div class="thumbcaption"><div class="magnify"><a href="/wiki/%ED%8C%8C%EC%9D%BC:Circle_Area.svg" class="internal" title="실제 크기로"></a></div>원의 넓이 = π × 반지름<sup>2</sup></div></div></div>
<div class="thumb tleft"><div class="thumbinner" style="width:174px;"><a href="/wiki/%ED%8C%8C%EC%9D%BC:CIRCLE_1_kor.png" class="image"><img alt="" src="//upload.wikimedia.org/wikipedia/commons/thumb/f/fb/CIRCLE_1_kor.png/172px-CIRCLE_1_kor.png" decoding="async" width="172" height="174" class="thumbimage" srcset="//upload.wikimedia.org/wikipedia/commons/thumb/f/fb/CIRCLE_1_kor.png/258px-CIRCLE_1_kor.png 1.5x, //upload.wikimedia.org/wikipedia/commons/thumb/f/fb/CIRCLE_1_kor.png/344px-CIRCLE_1_kor.png 2x" data-file-width="594" data-file-height="600" /></a> <div class="thumbcaption"><div class="magnify"><a href="/wiki/%ED%8C%8C%EC%9D%BC:CIRCLE_1_kor.png" class="internal" title="실제 크기로"></a></div>원의 둘레 = π × 지름</div></div></div>
<div class="thumb tleft"><div class="thumbinner" style="width:174px;"><a href="/wiki/%ED%8C%8C%EC%9D%BC:Squaring_the_circle.svg" class="image"><img alt="" src="//upload.wikimedia.org/wikipedia/commons/thumb/a/a7/Squaring_the_circle.svg/172px-Squaring_the_circle.svg.png" decoding="async" width="172" height="172" class="thumbimage" srcset="//upload.wikimedia.org/wikipedia/commons/thumb/a/a7/Squaring_the_circle.svg/258px-Squaring_the_circle.svg.png 1.5x, //upload.wikimedia.org/wikipedia/commons/thumb/a/a7/Squaring_the_circle.svg/344px-Squaring_the_circle.svg.png 2x" data-file-width="281" data-file-height="281" /></a> <div class="thumbcaption"><div class="magnify"><a href="/wiki/%ED%8C%8C%EC%9D%BC:Squaring_the_circle.svg" class="internal" title="실제 크기로"></a></div><a href="/wiki/%EC%9B%90%EC%A0%81%EB%AC%B8%EC%A0%9C" title="원적문제">원적문제</a></div></div></div>
<div class="thumb tleft"><div class="thumbinner" style="width:174px;"><a href="/wiki/%ED%8C%8C%EC%9D%BC:Circle_area_by_reassembly.svg" class="image"><img alt="" src="//upload.wikimedia.org/wikipedia/commons/thumb/1/16/Circle_area_by_reassembly.svg/172px-Circle_area_by_reassembly.svg.png" decoding="async" width="172" height="172" class="thumbimage" srcset="//upload.wikimedia.org/wikipedia/commons/thumb/1/16/Circle_area_by_reassembly.svg/258px-Circle_area_by_reassembly.svg.png 1.5x, //upload.wikimedia.org/wikipedia/commons/thumb/1/16/Circle_area_by_reassembly.svg/344px-Circle_area_by_reassembly.svg.png 2x" data-file-width="420" data-file-height="420" /></a> <div class="thumbcaption"><div class="magnify"><a href="/wiki/%ED%8C%8C%EC%9D%BC:Circle_area_by_reassembly.svg" class="internal" title="실제 크기로"></a></div>다빈치의 원의 넓이 계산</div></div></div>
<p>한편, 원주율은 계수가 <a href="/wiki/%EC%9C%A0%EB%A6%AC%EC%88%98" title="유리수">유리수</a>인 유한 차수 <a href="/wiki/%EB%8B%A4%ED%95%AD%EC%8B%9D" title="다항식">다항식</a>의 해가 될 수 없다. 이러한 종류의 수를 <a href="/wiki/%EC%B4%88%EC%9B%94%EC%88%98" title="초월수">초월수</a>라 부른다. 이 사실은 <a href="/wiki/1882%EB%85%84" title="1882년">1882년</a> <a href="/wiki/%ED%8E%98%EB%A5%B4%EB%94%94%EB%82%9C%ED%8A%B8_%ED%8F%B0_%EB%A6%B0%EB%8D%B0%EB%A7%8C" title="페르디난트 폰 린데만">페르디난트 폰 린데만</a>이 증명하였다. 여기에서 원주율은 어떤 <a href="/wiki/%EC%A0%95%EC%88%98" title="정수">정수</a>에 적당한 유리수를 곱하고 <a href="/wiki/%EC%A0%9C%EA%B3%B1%EA%B7%BC" title="제곱근">제곱근</a>을 씌우는 등의 <a href="/wiki/%EC%97%B0%EC%82%B0_(%EC%88%98%ED%95%99)" title="연산 (수학)">연산</a>을 조합하여 얻어낼 수 없다는 사실을 알 수 있다. 또한 원주율이 초월수라는 사실을 통해, <a href="/wiki/%EA%B3%A0%EB%8C%80_%EA%B7%B8%EB%A6%AC%EC%8A%A4" title="고대 그리스">그리스</a> 3대 난제 중 하나였던 “<a href="/wiki/%EC%9E%90_(%EB%8F%84%EA%B5%AC)" title="자 (도구)">자</a>와 <a href="/wiki/%EC%BB%B4%ED%8D%BC%EC%8A%A4" title="컴퍼스">컴퍼스</a>만을 사용하여 <a href="/wiki/%EC%9B%90_(%EA%B8%B0%ED%95%98%ED%95%99)" title="원 (기하학)">원</a>과 넓이가 같은 <a href="/wiki/%EC%A0%95%EC%82%AC%EA%B0%81%ED%98%95" title="정사각형">정사각형</a>을 <a href="/wiki/%EC%9E%91%EB%8F%84" class="mw-redirect" title="작도">작도</a>하는 <a href="/wiki/%EC%9B%90%EC%A0%81%EB%AC%B8%EC%A0%9C" title="원적문제">원적문제</a>”가 유한한 대수적 방법으로는 불가능하다는 것을 증명할 수 있다.
</p><p><a href="/wiki/%EC%9C%A0%ED%81%B4%EB%A6%AC%EB%93%9C_%EA%B8%B0%ED%95%98%ED%95%99" title="유클리드 기하학">유클리드 기하학</a>에서 원과 원주율의 관계를 살펴보면 다음과 같은 사실을 확인할 수 있다.<sup id="cite_ref-Rudin_8-0" class="reference"><a href="#cite_note-Rudin-8">[8]</a></sup><span class="reference plainlinksneverexpand" style="white-space:nowrap"><sup>:183</sup></span>
</p>
<ul><li>원의 둘레를 구하는 식은 원주율의 정의와 같다.</li></ul>
<dl><dd>원의 둘레 = 지름 × 원주율</dd></dl>
<ul><li>원의 넓이를 구하는 방법은 아르키메데스 시대 이후 여러 가지 기법이 알려져 있다. 널리 사용하는 방법 가운데 하나는 <a href="/wiki/%EB%A0%88%EC%98%A4%EB%82%98%EB%A5%B4%EB%8F%84_%EB%8B%A4%EB%B9%88%EC%B9%98" class="mw-redirect" title="레오나르도 다빈치">레오나르도 다빈치</a>가 고안한 것으로, <a href="/wiki/%EC%A0%95%EC%9C%A1%EA%B0%81%ED%98%95" class="mw-redirect" title="정육각형">정육각형</a>을 이용한 구적법이다. 레오나르도 다빈치는 왼쪽 그림과 같이 정육각형을 이용하여 분할한 원을 직사각형으로 치환하여 원의 넓이를 계산하였다.<sup id="cite_ref-9" class="reference"><a href="#cite_note-9">[9]</a></sup></li></ul>
<dl><dd>원의 넓이 = 원주율 × 반지름<sup>2</sup></dd></dl>
<p>원주율이 보이는 복잡한 수열에 비해 이를 계산하는 방법은 의외로 단순하다. <a href="/wiki/%EB%9D%BC%EC%9D%B4%ED%94%84%EB%8B%88%EC%B8%A0" class="mw-redirect" title="라이프니츠">라이프니츠</a>가 정리한 다음 계산식이 널리 알려져 있다.
</p>
<dl><dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \pi =4\left({\frac {1}{1}}-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+{\frac {1}{9}}-{\frac {1}{11}}+{\frac {1}{13}}-{\frac {1}{15}}+{\frac {1}{17}}-{\frac {1}{19}}+{\frac {1}{21}}-{\frac {1}{23}}+{\frac {1}{25}}-{\frac {1}{27}}+{\frac {1}{29}}-{\frac {1}{31}}+\cdots \right)}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>π<!-- π --></mi>
<mo>=</mo>
<mn>4</mn>
<mrow>
<mo>(</mo>
<mrow>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>1</mn>
</mfrac>
</mrow>
<mo>−<!-- − --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>3</mn>
</mfrac>
</mrow>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>5</mn>
</mfrac>
</mrow>
<mo>−<!-- − --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>7</mn>
</mfrac>
</mrow>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>9</mn>
</mfrac>
</mrow>
<mo>−<!-- − --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>11</mn>
</mfrac>
</mrow>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>13</mn>
</mfrac>
</mrow>
<mo>−<!-- − --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>15</mn>
</mfrac>
</mrow>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>17</mn>
</mfrac>
</mrow>
<mo>−<!-- − --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>19</mn>
</mfrac>
</mrow>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>21</mn>
</mfrac>
</mrow>
<mo>−<!-- − --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>23</mn>
</mfrac>
</mrow>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>25</mn>
</mfrac>
</mrow>
<mo>−<!-- − --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>27</mn>
</mfrac>
</mrow>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>29</mn>
</mfrac>
</mrow>
<mo>−<!-- − --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>31</mn>
</mfrac>
</mrow>
<mo>+</mo>
<mo>⋯<!-- ⋯ --></mo>
</mrow>
<mo>)</mo>
</mrow>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle \pi =4\left({\frac {1}{1}}-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+{\frac {1}{9}}-{\frac {1}{11}}+{\frac {1}{13}}-{\frac {1}{15}}+{\frac {1}{17}}-{\frac {1}{19}}+{\frac {1}{21}}-{\frac {1}{23}}+{\frac {1}{25}}-{\frac {1}{27}}+{\frac {1}{29}}-{\frac {1}{31}}+\cdots \right)}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/faff560c11dd1fb7ad1fd2a3086b577a2af6c0fd" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -2.505ex; width:102.335ex; height:6.176ex;" alt="\pi =4\left({\frac {1}{1}}-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+{\frac {1}{9}}-{\frac {1}{11}}+{\frac {1}{13}}-{\frac {1}{15}}+{\frac {1}{17}}-{\frac {1}{19}}+{\frac {1}{21}}-{\frac {1}{23}}+{\frac {1}{25}}-{\frac {1}{27}}+{\frac {1}{29}}-{\frac {1}{31}}+\cdots \right)"/></span></dd></dl>
<h2><span id=".EC.97.AD.EC.82.AC"></span><span class="mw-headline" id="역사">역사</span><span class="mw-editsection"><span class="mw-editsection-bracket">[</span><a href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8&action=edit&section=2" title="부분 편집: 역사">편집</a><span class="mw-editsection-bracket">]</span></span></h2>
<h3><span id=".EA.B3.A0.EB.8C.80"></span><span class="mw-headline" id="고대">고대</span><span class="mw-editsection"><span class="mw-editsection-bracket">[</span><a href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8&action=edit&section=3" title="부분 편집: 고대">편집</a><span class="mw-editsection-bracket">]</span></span></h3>
<p>고대의 여러 문화에서 원주율의 값으로 <a href="/wiki/3" title="3">3</a>이 쓰였다. 고대 <a href="/wiki/%EB%A9%94%EC%86%8C%ED%8F%AC%ED%83%80%EB%AF%B8%EC%95%84" title="메소포타미아">메소포타미아</a>에서도 원주율을 3으로 계산하였고<sup id="cite_ref-김흥식_10-0" class="reference"><a href="#cite_note-김흥식-10">[10]</a></sup>, <a href="/wiki/%EA%B5%AC%EC%95%BD%EC%84%B1%EA%B2%BD" title="구약성경">구약성경</a> 열왕기상 7장 23절과 역대하 4장 2절에는 직경과 둘레의 길이를 기술하여 원주율이 3정도 임을 알고 있었다고 추측된다. <a href="/wiki/%EA%B3%A0%EB%8C%80_%EC%A4%91%EA%B5%AD" class="mw-redirect" title="고대 중국">고대 중국</a>의 수학책인 《<a href="/wiki/%EA%B5%AC%EC%9E%A5%EC%82%B0%EC%88%A0" title="구장산술">구장산술</a>》에서도 3을 원주율로 제시하였다. 《구장산술》에는 다음과 같은 문제가 실려 있다.<sup id="cite_ref-11" class="reference"><a href="#cite_note-11">[11]</a></sup>
</p>
<table class="wikitable" style="border: 2px solid #eeeeee; margin: 0 0 1em 1em;">
<tbody><tr>
<th>원문
</th>
<th>번역
</th></tr>
<tr>
<td>今有圓田周三十步經十步問爲田幾何<br />答曰七十五步
</td>
<td>둘레가 30걸음, 지름이 10걸음인 원 모양의 밭이 있다면 넓이는 얼마인가? <br />답: 75걸음²
</td></tr>
<tr>
<td colspan="2">원주율의 근삿값을 3.14로 할 때 오늘날의 계산은
<dl><dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \pi *5^{2}=3.14*5^{2}=78.5}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>π<!-- π --></mi>
<mo>∗<!-- ∗ --></mo>
<msup>
<mn>5</mn>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
<mo>=</mo>
<mn>3.14</mn>
<mo>∗<!-- ∗ --></mo>
<msup>
<mn>5</mn>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
<mo>=</mo>
<mn>78.5</mn>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle \pi *5^{2}=3.14*5^{2}=78.5}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/797d2017c2661e1918656f192d4bdb7b8db90928" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.338ex; width:24.62ex; height:2.676ex;" alt="\pi *5^{2}=3.14*5^{2}=78.5"/></span></dd></dl>
</td></tr></tbody></table><p>
구장산술의 계산은 평균값으로 이루어져있다. (1) 원둘레가 30보인 경우 반지름은 30=2r*3.14 r=4.78 이경우의 면적은 71.74 (2) 지름이 10보인 경우 면적은 78.5. (1)과 (2)의 평균은 75보. 그러므로 구장산술의 계산이 부정확하다는 것은 잘못되었다.</p><div class="thumb tleft"><div class="thumbinner" style="width:152px;"><a href="/wiki/%ED%8C%8C%EC%9D%BC:Hagalaz.jpg" class="image"><img alt="" src="//upload.wikimedia.org/wikipedia/commons/1/1b/Hagalaz.jpg" decoding="async" width="150" height="150" class="thumbimage" data-file-width="150" data-file-height="150" /></a> <div class="thumbcaption"><div class="magnify"><a href="/wiki/%ED%8C%8C%EC%9D%BC:Hagalaz.jpg" class="internal" title="실제 크기로"></a></div>원에 내접하는 정육각형</div></div></div>
<p>구장산술에 실린 계산이 매우 부정확하다는 것은 왼쪽 그림을 보면 쉽게 알 수 있다. 지름이 1인 원에 내접하는 정육각형의 둘레는 3이고 실제 원의 둘레는 그것과는 차이가 상당하기 때문이다.<sup id="cite_ref-12" class="reference"><a href="#cite_note-12">[12]</a></sup> 이는 <a href="/wiki/%EA%B3%A0%EB%8C%80" class="mw-redirect" title="고대">고대</a>에서부터 이미 널리 알려진 문제였고 값을 보다 정확하게 구하기 위한 노력이 계속되었다. <a href="/wiki/%EA%B3%A0%EB%8C%80_%EC%9D%B4%EC%A7%91%ED%8A%B8" title="고대 이집트">고대 이집트</a>에서는 원통형 바퀴를 굴려 직접 측정해 원주율을 계산하였는데 <span class="nowrap"> </span><span class="frac nowrap" lang="en"><sup>256</sup>⁄<sub>81</sub></span>=3.16049……를 사용하였다.<sup id="cite_ref-김흥식_10-1" class="reference"><a href="#cite_note-김흥식-10">[10]</a></sup>
</p>
<div class="thumb tright"><div class="thumbinner" style="width:222px;"><a href="/wiki/%ED%8C%8C%EC%9D%BC:Archimedes_pi.svg" class="image"><img alt="" src="//upload.wikimedia.org/wikipedia/commons/thumb/c/c9/Archimedes_pi.svg/220px-Archimedes_pi.svg.png" decoding="async" width="220" height="73" class="thumbimage" srcset="//upload.wikimedia.org/wikipedia/commons/thumb/c/c9/Archimedes_pi.svg/330px-Archimedes_pi.svg.png 1.5x, //upload.wikimedia.org/wikipedia/commons/thumb/c/c9/Archimedes_pi.svg/440px-Archimedes_pi.svg.png 2x" data-file-width="750" data-file-height="250" /></a> <div class="thumbcaption"><div class="magnify"><a href="/wiki/%ED%8C%8C%EC%9D%BC:Archimedes_pi.svg" class="internal" title="실제 크기로"></a></div>원에 외접하는 다각형과 내접하는 다각형의 둘레를 이용한 아르키메데스의 원주율 계산</div></div></div>
<p>한편 기원전 3세기의 <a href="/wiki/%EA%B3%A0%EB%8C%80_%EA%B7%B8%EB%A6%AC%EC%8A%A4" title="고대 그리스">고대 그리스</a> 수학자 <a href="/wiki/%EC%95%84%EB%A5%B4%ED%82%A4%EB%A9%94%EB%8D%B0%EC%8A%A4" title="아르키메데스">아르키메데스</a>는 근대 <a href="/wiki/%EC%A0%81%EB%B6%84" title="적분">적분</a>이 없었던 당시에 <a href="/wiki/%EB%AC%B4%ED%95%9C%EC%86%8C" title="무한소">무한소</a>라는 개념을 사용하였다. 그는 <a href="/wiki/%EC%86%8C%EA%B1%B0%EB%B2%95" title="소거법">소거법</a>을 사용하여 <span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \pi }">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>π<!-- π --></mi>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle \pi }</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/9be4ba0bb8df3af72e90a0535fabcc17431e540a" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.338ex; width:1.332ex; height:1.676ex;" alt="\pi"/></span>의 <a href="/wiki/%EA%B7%BC%EC%82%BF%EA%B0%92" title="근삿값">근삿값</a>을 계산하였다. 이 방법은 임의 차원의 미지항에 대해 <a href="/wiki/%ED%95%A8%EC%88%98%EC%9D%98_%EA%B7%B9%ED%95%9C" title="함수의 극한">극한</a>을 취하는 것으로, <a href="/wiki/%EA%B7%80%EB%A5%98%EB%B2%95" title="귀류법">귀류법</a>을 사용하여 동일한 계산을 반복하는 과정을 통해 해답을 얻는 것이다. 아르키메데스는 변이 매우 많은 <a href="/wiki/%EB%8B%A4%EA%B0%81%ED%98%95" title="다각형">다각형</a>이 임의의 <a href="/wiki/%EC%9B%90_(%EA%B8%B0%ED%95%98%ED%95%99)" title="원 (기하학)">원</a>에 내접하는 경우와 외접하는 경우를 비교하여 원주율을 계산하였다. 즉, 임의의 원의 둘레는 그것에 외접하는 다각형의 둘레보다 짧고 내접하는 다각형보다 길다. 이때 다각형의 변이 많아질수록 외접하는 경우와 내접하는 경우의 둘레 차는 작아지므로 원의 둘레에 근사한다. 즉, 지름이 d인 원에 내접하는 변의 개수가 n인 <a href="/wiki/%EC%A0%95%EB%8B%A4%EA%B0%81%ED%98%95" title="정다각형">정다각형</a>의 둘레 P<sub>n</sub>에 대해 다음과 같이 <a href="/wiki/%ED%95%A8%EC%88%98%EC%9D%98_%EA%B7%B9%ED%95%9C" title="함수의 극한">함수의 극한</a>을 취하면 원주율을 얻을 수 있다.
</p>
<dl><dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \pi =\lim _{n\to \infty }{\frac {P_{n}}{d}}.}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>π<!-- π --></mi>
<mo>=</mo>
<munder>
<mo movablelimits="true" form="prefix">lim</mo>
<mrow class="MJX-TeXAtom-ORD">
<mi>n</mi>
<mo stretchy="false">→<!-- → --></mo>
<mi mathvariant="normal">∞<!-- ∞ --></mi>
</mrow>
</munder>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<msub>
<mi>P</mi>
<mrow class="MJX-TeXAtom-ORD">
<mi>n</mi>
</mrow>
</msub>
<mi>d</mi>
</mfrac>
</mrow>
<mo>.</mo>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle \pi =\lim _{n\to \infty }{\frac {P_{n}}{d}}.}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/ef45806eea40b08ab7d37374f45db54673d2508a" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -2.005ex; width:13.284ex; height:5.343ex;" alt="\pi =\lim _{{n\to \infty }}{\frac {P_{{n}}}{d}}."/></span></dd></dl>
<p>아르키메데스는 정구십육각형을 이용하여 <span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \pi }">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>π<!-- π --></mi>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle \pi }</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/9be4ba0bb8df3af72e90a0535fabcc17431e540a" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.338ex; width:1.332ex; height:1.676ex;" alt="\pi"/></span>의 값을 다음과 같이 계산하였다.<sup id="cite_ref-13" class="reference"><a href="#cite_note-13">[13]</a></sup>
</p>
<dl><dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle 3{\frac {10}{71}}<\pi <3{\frac {1}{7}}\approx 3.1408<\pi <3.1429}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mn>3</mn>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>10</mn>
<mn>71</mn>
</mfrac>
</mrow>
<mo><</mo>
<mi>π<!-- π --></mi>
<mo><</mo>
<mn>3</mn>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>7</mn>
</mfrac>
</mrow>
<mo>≈<!-- ≈ --></mo>
<mn>3.1408</mn>
<mo><</mo>
<mi>π<!-- π --></mi>
<mo><</mo>
<mn>3.1429</mn>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle 3{\frac {10}{71}}<\pi <3{\frac {1}{7}}\approx 3.1408<\pi <3.1429}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/5fa8bc8e5c61832a7a4c53b57261d52a40e2cf3b" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -2.005ex; width:38.559ex; height:5.343ex;" alt="3{\frac {10}{71}}<\pi <3{\frac {1}{7}}\approx 3.1408<\pi <3.1429"/></span></dd></dl>
<p>아르키메데스는 이 결과에 따라 <span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \pi }">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>π<!-- π --></mi>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle \pi }</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/9be4ba0bb8df3af72e90a0535fabcc17431e540a" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.338ex; width:1.332ex; height:1.676ex;" alt="\pi"/></span>의 근삿값으로 3.1416을 제시하였다. 또한, 아르키메데스는 원의 면적이 <span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \pi r^{2}}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>π<!-- π --></mi>
<msup>
<mi>r</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle \pi r^{2}}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/cd37db3982ad4e1157dcf8ddbfb280e7bae3b192" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.338ex; width:3.435ex; height:2.676ex;" alt="\pi r^{2}"/></span>임을 증명하였다. 아르키메데스는 자신의 저서 《구와 원기둥》에서 어떠한 크기가 주어지더라도 임의의 크기에 적당한 수를 곱하여 주어진 크기를 초과할 수 있다고 가정하였다. 이를 <a href="/wiki/%EC%8B%A4%EC%88%98" title="실수">실수</a>에서의 <a href="/wiki/%EC%95%84%EB%A5%B4%ED%82%A4%EB%A9%94%EB%8D%B0%EC%8A%A4_%EC%84%B1%EC%A7%88" title="아르키메데스 성질">아르키메데스 성질</a>이라고 한다.<sup id="cite_ref-14" class="reference"><a href="#cite_note-14">[14]</a></sup>
</p><p>중국의 <a href="/wiki/%EC%82%BC%EA%B5%AD%EC%8B%9C%EB%8C%80_(%EC%A4%91%EA%B5%AD)" class="mw-redirect" title="삼국시대 (중국)">삼국시대</a> <a href="/wiki/%EC%9C%84_(%EC%82%BC%EA%B5%AD)" title="위 (삼국)">위나라</a> 수학자 <a href="/wiki/%EC%9C%A0%ED%9C%98" title="유휘">유휘</a>는 《구장산술》에 주해를 달아 다시 출판하였는데, 아르키메데스와 같은 방법을 사용하여 원주율을 <span class="nowrap"> </span><span class="frac nowrap" lang="en"><sup>157</sup>⁄<sub>50</sub></span>=3.14 로 계산하였다. 유휘가 계산한 원주율 근삿값은 오늘날에도 일상생활에서 사용한다.<sup id="cite_ref-15" class="reference"><a href="#cite_note-15">[15]</a></sup>
</p><p>2세기에 들어 중국의 장형은 원주율을 3.1623으로 계산하였고<sup id="cite_ref-16" class="reference"><a href="#cite_note-16">[16]</a></sup> 5세기 중국 <a href="/wiki/%EB%82%A8%EB%B6%81%EC%A1%B0_%EC%8B%9C%EB%8C%80" title="남북조 시대">남북조 시대</a> <a href="/wiki/%EC%86%A1_(%EB%82%A8%EC%A1%B0)" title="송 (남조)">송나라</a>의 <a href="/wiki/%EC%A1%B0%EC%B6%A9%EC%A7%80" title="조충지">조충지</a>는 3.141592로 계산하였다.<sup id="cite_ref-17" class="reference"><a href="#cite_note-17">[17]</a></sup> 독일에서는 1600년대 <a href="/wiki/%EB%A4%BC%EB%8F%8C%ED%94%84_%ED%8C%90_%EC%BE%B0%EB%9F%B0" title="뤼돌프 판 쾰런">뤼돌프 판 쾰런</a>이 소수점 이하 35자리까지 계산하였다.<sup id="cite_ref-사이언스타임즈_3-1" class="reference"><a href="#cite_note-사이언스타임즈-3">[3]</a></sup> 컴퓨터를 도입하기 이전에 가장 긴 자리수의 원주율을 계산한 사람은 영국의 수학자 샹크스였다. 그는 15년이나 걸려 1873년께 소수점 이하 707자리까지 원주율 값을 계산해냈다. 하지만 후에 그 계산은 528자리까지만 정확한 것으로 밝혀졌다.<sup id="cite_ref-국민일보_18-0" class="reference"><a href="#cite_note-국민일보-18">[18]</a></sup>
</p>
<h3><span id=".EC.BB.B4.ED.93.A8.ED.84.B0.EB.A5.BC_.ED.86.B5.ED.95.9C_.EC.9B.90.EC.A3.BC.EC.9C.A8_.EA.B3.84.EC.82.B0"></span><span class="mw-headline" id="컴퓨터를_통한_원주율_계산">컴퓨터를 통한 원주율 계산</span><span class="mw-editsection"><span class="mw-editsection-bracket">[</span><a href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8&action=edit&section=4" title="부분 편집: 컴퓨터를 통한 원주율 계산">편집</a><span class="mw-editsection-bracket">]</span></span></h3>
<p><a href="/wiki/1949%EB%85%84" title="1949년">1949년</a> 9월 최초로 <a href="/wiki/%EC%BB%B4%ED%93%A8%ED%84%B0" title="컴퓨터">컴퓨터</a>를 이용하여 70시간에 걸쳐 소수점 아래 2,037자리까지 계산하였다. 원주율 계산에 컴퓨터를 도입한 이후 원주율 계산은 단순 <a href="/wiki/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98" title="알고리즘">알고리즘</a>의 무한 반복에 불과한 작업이 되어 수학적 의미를 잃었다.<sup id="cite_ref-사이먼_19-0" class="reference"><a href="#cite_note-사이먼-19">[19]</a></sup> 이 계산은 종종 컴퓨터의 성능을 시험하기 위한 방법으로 사용한다.<sup id="cite_ref-국민일보_18-1" class="reference"><a href="#cite_note-국민일보-18">[18]</a></sup> 2005년 일본 <a href="/wiki/%EB%8F%84%EC%BF%84_%EB%8C%80%ED%95%99" title="도쿄 대학">도쿄 대학</a>의 가네다 야스마사 교수는 컴퓨터를 601시간 56분 동안 사용하여 원주율을 소수점 1,241,100,000,000자리까지 구하였다. 2009년 〈도쿄신문〉에 따르면, 일본 <a href="/wiki/%EC%93%B0%EC%BF%A0%EB%B0%94_%EB%8C%80%ED%95%99" title="쓰쿠바 대학">쓰쿠바 대학</a> 계산과학연구센터는 17일, 슈퍼컴퓨터를 사용한 원주율 계산에서, 2조 5769억 8037만 자리수의 세계기록을 수립했다고 한다. (73시간 59분 소요)<sup id="cite_ref-20" class="reference"><a href="#cite_note-20">[20]</a></sup><sup id="cite_ref-21" class="reference"><a href="#cite_note-21">[21]</a></sup> 그 이후 프랑스에서는 2조 7천억 자리까지 계산하였다.<sup id="cite_ref-22" class="reference"><a href="#cite_note-22">[22]</a></sup> 2010년 8월 3일에는 일본의 회사원 곤도 시게루(近藤茂)가 소수점 이하 5조 자리까지 계산하였다. (90일 7시간 소요, 검증 기간 포함 / PC 사용)<sup id="cite_ref-23" class="reference"><a href="#cite_note-23">[23]</a></sup> 2016년 11월 11일 스위스의 입자 물리학자인 페터 트뤼프(Peter Trüb)는 105일 동안 계산하여, 원주율을 소수점 이하 22조 4591억 5771만 8361자리(<span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \pi ^{e}}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<msup>
<mi>π<!-- π --></mi>
<mrow class="MJX-TeXAtom-ORD">
<mi>e</mi>
</mrow>
</msup>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle \pi ^{e}}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/eb60fab89f41a1248e5d94a6f3d338b862c77a19" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.338ex; width:2.333ex; height:2.343ex;" alt="{\displaystyle \pi ^{e}}"/></span>조 개)까지 계산했다.<sup id="cite_ref-24" class="reference"><a href="#cite_note-24">[24]</a></sup>
</p>
<h2><span id=".EC.9B.90.EC.A3.BC.EC.9C.A8.EC.9D.98_.EA.B0.92"></span><span class="mw-headline" id="원주율의_값">원주율의 값</span><span class="mw-editsection"><span class="mw-editsection-bracket">[</span><a href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8&action=edit&section=5" title="부분 편집: 원주율의 값">편집</a><span class="mw-editsection-bracket">]</span></span></h2>
<p><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \pi }">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>π<!-- π --></mi>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle \pi }</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/9be4ba0bb8df3af72e90a0535fabcc17431e540a" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.338ex; width:1.332ex; height:1.676ex;" alt="\pi"/></span> 값의 소수점 아래 1,000자리 수는 다음과 같다.
</p>
<pre>3.1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679
8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196
4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273
7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094
3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912
9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132
0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235
4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859
5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303
5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989...
</pre>
<p><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \pi }">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>π<!-- π --></mi>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle \pi }</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/9be4ba0bb8df3af72e90a0535fabcc17431e540a" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.338ex; width:1.332ex; height:1.676ex;" alt="\pi"/></span> 값의 소수점 아래 100만 자리, 10억 자리, 1조 자리 수는 <a rel="nofollow" class="external text" href="http://pi2e.ch/blog/2017/03/10/pi-digits-download/">Peter Trüb의 웹사이트</a>에서 다운로드 받을 수 있다.
</p><p>또는 <a rel="nofollow" class="external text" href="http://0xf.kr/pi/">다른 웹사이트</a><sup class="정리_필요 noprint">[<a href="/wiki/%EC%9C%84%ED%82%A4%EB%B0%B1%EA%B3%BC:%EA%B9%A8%EC%A7%84_%EB%A7%81%ED%81%AC" title="위키백과:깨진 링크">깨진 링크</a>(<a rel="nofollow" class="external text" href="http://web.archive.org/web/*/http://0xf.kr/pi/">과거 내용 찾기</a>)]</sup> 에서도 확인할 수 있다.
</p>
<h2><span id=".EC.88.98.ED.95.99.EC.A0.81_.ED.8A.B9.EC.84.B1"></span><span class="mw-headline" id="수학적_특성">수학적 특성</span><span class="mw-editsection"><span class="mw-editsection-bracket">[</span><a href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8&action=edit&section=6" title="부분 편집: 수학적 특성">편집</a><span class="mw-editsection-bracket">]</span></span></h2>
<p>원주율은 두 <a href="/wiki/%EC%A0%95%EC%88%98" title="정수">정수</a>의 비로 나타낼 수 없는 <a href="/wiki/%EB%AC%B4%EB%A6%AC%EC%88%98" title="무리수">무리수</a>이다. 또한, <a href="/wiki/%EA%B3%84%EC%88%98" title="계수">계수</a>가 <a href="/wiki/%EC%9C%A0%EB%A6%AC%EC%88%98" title="유리수">유리수</a>인 <a href="/wiki/%EB%8B%A4%ED%95%AD%EC%8B%9D" title="다항식">다항식</a>의 <a href="/wiki/%EA%B7%BC_(%EC%88%98%ED%95%99)" title="근 (수학)">근</a>이 될 수 없는 <a href="/wiki/%EC%B4%88%EC%9B%94%EC%88%98" title="초월수">초월수</a>이다.
</p>
<h3><span id=".EB.AC.B4.EB.A6.AC.EC.88.98"></span><span class="mw-headline" id="무리수">무리수</span><span class="mw-editsection"><span class="mw-editsection-bracket">[</span><a href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8&action=edit&section=7" title="부분 편집: 무리수">편집</a><span class="mw-editsection-bracket">]</span></span></h3>
<div class="rellink boilerplate seealso"><img alt="" src="//upload.wikimedia.org/wikipedia/commons/thumb/e/ec/Crystal_Clear_app_xmag.svg/16px-Crystal_Clear_app_xmag.svg.png" decoding="async" width="16" height="16" srcset="//upload.wikimedia.org/wikipedia/commons/thumb/e/ec/Crystal_Clear_app_xmag.svg/24px-Crystal_Clear_app_xmag.svg.png 1.5x, //upload.wikimedia.org/wikipedia/commons/thumb/e/ec/Crystal_Clear_app_xmag.svg/32px-Crystal_Clear_app_xmag.svg.png 2x" data-file-width="128" data-file-height="128" /> <a href="/wiki/%EC%9B%90%EC%A3%BC%EC%9C%A8%EC%9D%98_%EB%AC%B4%EB%A6%AC%EC%84%B1_%EC%A6%9D%EB%AA%85" title="원주율의 무리성 증명">원주율의 무리성 증명</a> 문서를 참고하십시오.</div>
<p>원주율이 <a href="/wiki/%EB%AC%B4%EB%A6%AC%EC%88%98" title="무리수">무리수</a>라는 것은 1761년에 <a href="/w/index.php?title=%EC%9A%94%ED%95%9C_%ED%95%98%EC%9D%B8%EB%A6%AC%ED%9E%88_%EB%9E%8C%EB%B2%A0%EB%A5%B4%ED%8A%B8&action=edit&redlink=1" class="new" title="요한 하인리히 람베르트 (없는 문서)">요한 하인리히 람베르트</a>가 증명했다.<sup id="cite_ref-25" class="reference"><a href="#cite_note-25">[25]</a></sup> 람베르트는 다음과 같이 <a href="/wiki/%ED%83%84%EC%A0%A0%ED%8A%B8" class="mw-redirect" title="탄젠트">탄젠트</a> 함수의 <a href="/wiki/%EC%97%B0%EB%B6%84%EC%88%98" title="연분수">연분수</a> 전개식을 이용하여 이를 증명하였다.<sup id="cite_ref-26" class="reference"><a href="#cite_note-26">[26]</a></sup>
</p>
<dl><dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \tan(x)={\cfrac {x}{1-{\cfrac {x^{2}}{3-{\cfrac {x^{2}}{5-{\cfrac {x^{2}}{7-{}\ddots }}}}}}}}}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>tan</mi>
<mo>⁡<!-- --></mo>
<mo stretchy="false">(</mo>
<mi>x</mi>
<mo stretchy="false">)</mo>
<mo>=</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mrow>
<mpadded width="0" height="8.6pt" depth="3pt">
<mrow />
</mpadded>
<mstyle displaystyle="false" scriptlevel="0">
<mrow class="MJX-TeXAtom-ORD">
<mi>x</mi>
</mrow>
</mstyle>
</mrow>
<mrow>
<mpadded width="0" height="8.6pt" depth="3pt">
<mrow />
</mpadded>
<mstyle displaystyle="false" scriptlevel="0">
<mrow class="MJX-TeXAtom-ORD">
<mn>1</mn>
<mo>−<!-- − --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mrow>
<mpadded width="0" height="8.6pt" depth="3pt">
<mrow />
</mpadded>
<mstyle displaystyle="false" scriptlevel="0">
<mrow class="MJX-TeXAtom-ORD">
<msup>
<mi>x</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
</mrow>
</mstyle>
</mrow>
<mrow>
<mpadded width="0" height="8.6pt" depth="3pt">
<mrow />
</mpadded>
<mstyle displaystyle="false" scriptlevel="0">
<mrow class="MJX-TeXAtom-ORD">
<mn>3</mn>
<mo>−<!-- − --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mrow>
<mpadded width="0" height="8.6pt" depth="3pt">
<mrow />
</mpadded>
<mstyle displaystyle="false" scriptlevel="0">
<mrow class="MJX-TeXAtom-ORD">
<msup>
<mi>x</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
</mrow>
</mstyle>
</mrow>
<mrow>
<mpadded width="0" height="8.6pt" depth="3pt">
<mrow />
</mpadded>
<mstyle displaystyle="false" scriptlevel="0">
<mrow class="MJX-TeXAtom-ORD">
<mn>5</mn>
<mo>−<!-- − --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mrow>
<mpadded width="0" height="8.6pt" depth="3pt">
<mrow />
</mpadded>
<mstyle displaystyle="false" scriptlevel="0">
<mrow class="MJX-TeXAtom-ORD">
<msup>
<mi>x</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
</mrow>
</mstyle>
</mrow>
<mrow>
<mpadded width="0" height="8.6pt" depth="3pt">
<mrow />
</mpadded>
<mstyle displaystyle="false" scriptlevel="0">
<mrow class="MJX-TeXAtom-ORD">
<mn>7</mn>
<mo>−<!-- − --></mo>
<mrow class="MJX-TeXAtom-ORD">
</mrow>
<mo>⋱<!-- ⋱ --></mo>
</mrow>
</mstyle>
</mrow>
</mfrac>
</mrow>
</mrow>
</mstyle>
</mrow>
</mfrac>
</mrow>
</mrow>
</mstyle>
</mrow>
</mfrac>
</mrow>
</mrow>
</mstyle>
</mrow>
</mfrac>
</mrow>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle \tan(x)={\cfrac {x}{1-{\cfrac {x^{2}}{3-{\cfrac {x^{2}}{5-{\cfrac {x^{2}}{7-{}\ddots }}}}}}}}}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/629461e9c7f83aff313c263aadb4f76ca7cb179e" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -15.338ex; width:32.319ex; height:19.509ex;" alt="{\displaystyle \tan(x)={\cfrac {x}{1-{\cfrac {x^{2}}{3-{\cfrac {x^{2}}{5-{\cfrac {x^{2}}{7-{}\ddots }}}}}}}}}"/></span></dd></dl>
<p>x가 0 이 아닌 <a href="/wiki/%EC%9C%A0%EB%A6%AC%EC%88%98" title="유리수">유리수</a>일 때 위에 전개된 연분수를 십진기수법으로 나타내면 언제나 순환하지 않는 소수이므로 항상 무리수이다. 한편, tan(<span class="nowrap"> </span><span class="frac nowrap" lang="en"><sup>π</sup>⁄<sub>4</sub></span>)=1 이므로 <span class="nowrap"> </span><span class="frac nowrap" lang="en"><sup>π</sup>⁄<sub>4</sub></span>는 반드시 무리수여만 한다. 따라서 π 역시 무리수이다.<sup id="cite_ref-27" class="reference"><a href="#cite_note-27">[27]</a></sup><sup id="cite_ref-28" class="reference"><a href="#cite_note-28">[주해 1]</a></sup>
</p>
<h3><span id=".EC.B4.88.EC.9B.94.EC.88.98"></span><span class="mw-headline" id="초월수">초월수</span><span class="mw-editsection"><span class="mw-editsection-bracket">[</span><a href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8&action=edit&section=8" title="부분 편집: 초월수">편집</a><span class="mw-editsection-bracket">]</span></span></h3>
<div class="thumb tright">
<div class="thumbinner" style="width:222px;"><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle e^{i\pi }+1=0\;\;\!}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<msup>
<mi>e</mi>
<mrow class="MJX-TeXAtom-ORD">
<mi>i</mi>
<mi>π<!-- π --></mi>
</mrow>
</msup>
<mo>+</mo>
<mn>1</mn>
<mo>=</mo>
<mn>0</mn>
<mspace width="thickmathspace" />
<mspace width="thickmathspace" />
<mspace width="negativethinmathspace" />
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle e^{i\pi }+1=0\;\;\!}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/8117181d905084cb45b806aa0dab34ca20c1da5d" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.505ex; margin-right: -0.387ex; width:12.379ex; height:2.843ex;" alt="{\displaystyle e^{i\pi }+1=0\;\;\!}"/></span>
<div class="thumbcaption"><a href="/wiki/%EC%98%A4%EC%9D%BC%EB%9F%AC_%EB%93%B1%EC%8B%9D" class="mw-redirect" title="오일러 등식">오일러 등식</a>은 기초 수학의 여러 개념에서 빈번하게 등장한다.</div></div></div>
<p>원주율이 <a href="/wiki/%EC%B4%88%EC%9B%94%EC%88%98" title="초월수">초월수</a>임은 <a href="/wiki/%EC%98%A4%EC%9D%BC%EB%9F%AC_%EB%93%B1%EC%8B%9D" class="mw-redirect" title="오일러 등식">오일러 등식</a>을 이용하여 다음과 같이 증명할 수 있다.<sup id="cite_ref-29" class="reference"><a href="#cite_note-29">[28]</a></sup> 오일러 등식은,
</p>
<dl><dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle e^{i\pi }+1=0\;\;\!}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<msup>
<mi>e</mi>
<mrow class="MJX-TeXAtom-ORD">
<mi>i</mi>
<mi>π<!-- π --></mi>
</mrow>
</msup>
<mo>+</mo>
<mn>1</mn>
<mo>=</mo>
<mn>0</mn>
<mspace width="thickmathspace" />
<mspace width="thickmathspace" />
<mspace width="negativethinmathspace" />
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle e^{i\pi }+1=0\;\;\!}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/8117181d905084cb45b806aa0dab34ca20c1da5d" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.505ex; margin-right: -0.387ex; width:12.379ex; height:2.843ex;" alt="{\displaystyle e^{i\pi }+1=0\;\;\!}"/></span> …… (1)<sup id="cite_ref-30" class="reference"><a href="#cite_note-30">[주해 2]</a></sup></dd></dl>
<p>이다. 이 때 π가 정계수 대수방정식 <span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \zeta (x)=0}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>ζ<!-- ζ --></mi>
<mo stretchy="false">(</mo>
<mi>x</mi>
<mo stretchy="false">)</mo>
<mo>=</mo>
<mn>0</mn>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle \zeta (x)=0}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/83059d221d81f4e1c202f5b2dca5707eb058a3bc" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.838ex; width:8.495ex; height:2.843ex;" alt="\zeta (x)=0"/></span>의 근이라면 <span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \zeta (\pi )=0}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>ζ<!-- ζ --></mi>
<mo stretchy="false">(</mo>
<mi>π<!-- π --></mi>
<mo stretchy="false">)</mo>
<mo>=</mo>
<mn>0</mn>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle \zeta (\pi )=0}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/f76d526f93eba0e77400b3a79c216eef852eb1f9" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.838ex; width:8.497ex; height:2.843ex;" alt="\zeta (\pi )=0"/></span>이다. 따라서 <span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \zeta (\pi )\cdot \zeta (-\pi )=0}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>ζ<!-- ζ --></mi>
<mo stretchy="false">(</mo>
<mi>π<!-- π --></mi>
<mo stretchy="false">)</mo>
<mo>⋅<!-- ⋅ --></mo>
<mi>ζ<!-- ζ --></mi>
<mo stretchy="false">(</mo>
<mo>−<!-- − --></mo>
<mi>π<!-- π --></mi>
<mo stretchy="false">)</mo>
<mo>=</mo>
<mn>0</mn>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle \zeta (\pi )\cdot \zeta (-\pi )=0}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/373a928d19bb260a82b9c9cbde576d11a15e0f16" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.838ex; width:16.221ex; height:2.843ex;" alt="\zeta (\pi )\cdot \zeta (-\pi )=0"/></span> 역시 성립하여야 한다. 이제 y=iπ라 하면 π=-iy 이고 -π=iy 이므로, iπ는 다음 식으로 나타낼 수 있는 정계수 대수방정식을 만족시켜야 한다.
</p>
<dl><dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \zeta (\pi )\cdot \zeta (-\pi )=\Psi (y)=0}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>ζ<!-- ζ --></mi>
<mo stretchy="false">(</mo>
<mi>π<!-- π --></mi>
<mo stretchy="false">)</mo>
<mo>⋅<!-- ⋅ --></mo>
<mi>ζ<!-- ζ --></mi>
<mo stretchy="false">(</mo>
<mo>−<!-- − --></mo>
<mi>π<!-- π --></mi>
<mo stretchy="false">)</mo>
<mo>=</mo>
<mi mathvariant="normal">Ψ<!-- Ψ --></mi>
<mo stretchy="false">(</mo>
<mi>y</mi>
<mo stretchy="false">)</mo>
<mo>=</mo>
<mn>0</mn>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle \zeta (\pi )\cdot \zeta (-\pi )=\Psi (y)=0}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/65e3ef01c54a87b5316df86838be88fb72e43b6f" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.838ex; width:24.092ex; height:2.843ex;" alt="\zeta (\pi )\cdot \zeta (-\pi )=\Psi (y)=0"/></span></dd></dl>
<p>이제 <span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \Psi (y)=0}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi mathvariant="normal">Ψ<!-- Ψ --></mi>
<mo stretchy="false">(</mo>
<mi>y</mi>
<mo stretchy="false">)</mo>
<mo>=</mo>
<mn>0</mn>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle \Psi (y)=0}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/8bf2fe8d7f62ef7fad482c3ac28c645c2723279a" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.838ex; width:9.034ex; height:2.843ex;" alt="\Psi (y)=0"/></span>을 ν차원의 방정식이라 하면 그 <a href="/wiki/%EA%B7%BC_(%EC%88%98%ED%95%99)" title="근 (수학)">근</a>인 y<sub>1</sub>, y<sub>2</sub>,……, y<sub>ν</sub>에는 iπ가 존재하여야 하므로, 식 (1)에 따라 다음과 같이 나타낼 수 있다.
</p>
<dl><dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle (1+e^{y_{1}})(1+e^{y_{2}})\cdots (1+e^{y_{\nu }})=0}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mo stretchy="false">(</mo>
<mn>1</mn>
<mo>+</mo>
<msup>
<mi>e</mi>
<mrow class="MJX-TeXAtom-ORD">
<msub>
<mi>y</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>1</mn>
</mrow>
</msub>
</mrow>
</msup>
<mo stretchy="false">)</mo>
<mo stretchy="false">(</mo>
<mn>1</mn>
<mo>+</mo>
<msup>
<mi>e</mi>
<mrow class="MJX-TeXAtom-ORD">
<msub>
<mi>y</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msub>
</mrow>
</msup>
<mo stretchy="false">)</mo>
<mo>⋯<!-- ⋯ --></mo>
<mo stretchy="false">(</mo>
<mn>1</mn>
<mo>+</mo>
<msup>
<mi>e</mi>
<mrow class="MJX-TeXAtom-ORD">
<msub>
<mi>y</mi>
<mrow class="MJX-TeXAtom-ORD">
<mi>ν<!-- ν --></mi>
</mrow>
</msub>
</mrow>
</msup>
<mo stretchy="false">)</mo>
<mo>=</mo>
<mn>0</mn>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle (1+e^{y_{1}})(1+e^{y_{2}})\cdots (1+e^{y_{\nu }})=0}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/af75e72a6b04a621c90f62e2413dd494beec4c28" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.838ex; width:34.093ex; height:2.843ex;" alt="(1+e^{{y_{{1}}}})(1+e^{{y_{{2}}}})\cdots (1+e^{{y_{{\nu }}}})=0"/></span></dd></dl>
<p>그런데 이러한 관계를 만족하는 대수방정식의 근이 유리수라고 가정하면 무한히 약분할 수 있어서, 이를 기약분수로 표현할 수 없는 모순이 생긴다.<sup id="cite_ref-31" class="reference"><a href="#cite_note-31">[주해 3]</a></sup> 유리수를 기약분수로 표현할 수 없다는 것은 유리수의 정의에 어긋나므로 π가 정계수 대수방정식 <span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \zeta (x)=0}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>ζ<!-- ζ --></mi>
<mo stretchy="false">(</mo>
<mi>x</mi>
<mo stretchy="false">)</mo>
<mo>=</mo>
<mn>0</mn>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle \zeta (x)=0}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/83059d221d81f4e1c202f5b2dca5707eb058a3bc" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.838ex; width:8.495ex; height:2.843ex;" alt="\zeta (x)=0"/></span>의 근이라는 최초의 가정이 잘못되었다고 볼 수밖에 없다. 즉, 원주율은 초월수이다. 자세한 증명은 링크한 주석을 참고하기 바란다.<sup id="cite_ref-32" class="reference"><a href="#cite_note-32">[29]</a></sup>
</p>
<h3><span id=".EC.88.98.EC.97.B4"></span><span class="mw-headline" id="수열">수열</span><span class="mw-editsection"><span class="mw-editsection-bracket">[</span><a href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8&action=edit&section=9" title="부분 편집: 수열">편집</a><span class="mw-editsection-bracket">]</span></span></h3>
<p>개요에서 밝혔듯이 원주율은 반복되지 않고 무한히 계속되는 수열을 이룬다. <a href="/wiki/%EB%84%A4%EB%8D%9C%EB%9E%80%EB%93%9C" title="네덜란드">네덜란드</a> 수학자 <a href="/wiki/%EB%9D%BC%EC%9C%84%ED%8A%B8%EC%A0%84_%EB%B8%8C%EB%9D%BC%EC%9A%B0%EC%96%B4%EB%A5%B4" class="mw-redirect" title="라위트전 브라우어르">라위트전 브라우어르</a>는 다음과 같은 질문을 제기하였다.<sup id="cite_ref-장우석_33-0" class="reference"><a href="#cite_note-장우석-33">[30]</a></sup>
</p>
<ul><li>원주율 π = 3.141592…… 의 전개에서 계속되는 소수의 수열에 9가 연속적으로 100회 나타날까?</li></ul>
<p>브라우어르는 이 수열이 무한히 계속되기 때문에 이 수열을 어느 정도까지만 확인한 결과만으로는 위 질문에 답할 수 없다는 점을 지적하였다. 실제 소수점 이하 762번째에서부터 수열 999999 가 출현한다. 이 수열은 <a href="/wiki/%ED%8C%8C%EC%9D%B8%EB%A7%8C_%ED%8F%AC%EC%9D%B8%ED%8A%B8" title="파인만 포인트">파인만 포인트</a>로 알려져 있으며 원주율의 소수점 이하 수열에서 확률 0.08%로 발견할 수 있는 것으로 알려져 있다.<sup id="cite_ref-34" class="reference"><a href="#cite_note-34">[31]</a></sup> 따라서 경험적 방법으로는 위 문제에 답할 수 없다. 브라우어르는 이러한 논의를 바탕으로 <a href="/wiki/%EC%95%84%EB%A6%AC%EC%8A%A4%ED%86%A0%ED%85%94%EB%A0%88%EC%8A%A4" title="아리스토텔레스">아리스토텔레스</a>의 배중률<sup id="cite_ref-35" class="reference"><a href="#cite_note-35">[주해 4]</a></sup> 은 유한한 개수를 대상으로 한 것에만 적용 수 있을 뿐 무한한 것에 적용할 수 없다고 결론지었다.<sup id="cite_ref-장우석_33-1" class="reference"><a href="#cite_note-장우석-33">[30]</a></sup>
</p><p>원주율에서 나타나는 수열은 무작위 <a href="/wiki/%ED%91%9C%EC%A7%91" title="표집">표집</a>을 사용해 만든 난수표의 성질을 보인다. 하지만, 실제 원주율의 수열이 완전한 무작위성을 보이는지는 증명되지 않았다.<sup id="cite_ref-sciencedaily.com_7-1" class="reference"><a href="#cite_note-sciencedaily.com-7">[7]</a></sup>
</p>
<h2><span id=".EA.B3.84.EC.82.B0.EC.8B.9D"></span><span class="mw-headline" id="계산식">계산식</span><span class="mw-editsection"><span class="mw-editsection-bracket">[</span><a href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8&action=edit&section=10" title="부분 편집: 계산식">편집</a><span class="mw-editsection-bracket">]</span></span></h2>
<p>원주율은 <a href="/wiki/%EB%AC%B4%EB%A6%AC%EC%88%98" title="무리수">무리수</a>이기 때문에 그 값은 근삿값으로밖에 알 수 없다. 대부분의 계산에는 3.14나 22/7 라는 근삿값을 사용해도 충분하다. 355/113은 외우기 좋고, 정밀도도 좋다. 좀 더 정밀한 기술의 계산에서는 3.1416 또는 3.14159 등을 사용하기도 한다. 기상 예보나 인공 위성 등의 계산에는 소수점 아래 30자리까지 나아간 근삿값을 사용하고 있다. 이렇게 불규칙적인 패턴을 가지는 원주율은 다음과 같이 규칙적인 수식을 이용하여 계산할 수 있다. 더 정확한 값을 얻으려면 수식을 연장하기만 하면 된다.<sup id="cite_ref-사이먼_19-1" class="reference"><a href="#cite_note-사이먼-19">[19]</a></sup>
</p>
<dl><dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \pi =4\left({\frac {1}{1}}-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+{\frac {1}{9}}-{\frac {1}{11}}+{\frac {1}{13}}-{\frac {1}{15}}+{\frac {1}{17}}-{\frac {1}{19}}+{\frac {1}{21}}-{\frac {1}{23}}+{\frac {1}{25}}-{\frac {1}{27}}+{\frac {1}{29}}-{\frac {1}{31}}+{\frac {1}{33}}-\cdots \right)}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>π<!-- π --></mi>
<mo>=</mo>
<mn>4</mn>
<mrow>
<mo>(</mo>
<mrow>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>1</mn>
</mfrac>
</mrow>
<mo>−<!-- − --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>3</mn>
</mfrac>
</mrow>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>5</mn>
</mfrac>
</mrow>
<mo>−<!-- − --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>7</mn>
</mfrac>
</mrow>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>9</mn>
</mfrac>
</mrow>
<mo>−<!-- − --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>11</mn>
</mfrac>
</mrow>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>13</mn>
</mfrac>
</mrow>
<mo>−<!-- − --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>15</mn>
</mfrac>
</mrow>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>17</mn>
</mfrac>
</mrow>
<mo>−<!-- − --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>19</mn>
</mfrac>
</mrow>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>21</mn>
</mfrac>
</mrow>
<mo>−<!-- − --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>23</mn>
</mfrac>
</mrow>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>25</mn>
</mfrac>
</mrow>
<mo>−<!-- − --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>27</mn>
</mfrac>
</mrow>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>29</mn>
</mfrac>
</mrow>
<mo>−<!-- − --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>31</mn>
</mfrac>
</mrow>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>33</mn>
</mfrac>
</mrow>
<mo>−<!-- − --></mo>
<mo>⋯<!-- ⋯ --></mo>
</mrow>
<mo>)</mo>
</mrow>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle \pi =4\left({\frac {1}{1}}-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+{\frac {1}{9}}-{\frac {1}{11}}+{\frac {1}{13}}-{\frac {1}{15}}+{\frac {1}{17}}-{\frac {1}{19}}+{\frac {1}{21}}-{\frac {1}{23}}+{\frac {1}{25}}-{\frac {1}{27}}+{\frac {1}{29}}-{\frac {1}{31}}+{\frac {1}{33}}-\cdots \right)}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/92d37391d219e5689f027cf34064045f204e1533" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -2.505ex; width:108.337ex; height:6.176ex;" alt="\pi =4\left({\frac {1}{1}}-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+{\frac {1}{9}}-{\frac {1}{11}}+{\frac {1}{13}}-{\frac {1}{15}}+{\frac {1}{17}}-{\frac {1}{19}}+{\frac {1}{21}}-{\frac {1}{23}}+{\frac {1}{25}}-{\frac {1}{27}}+{\frac {1}{29}}-{\frac {1}{31}}+{\frac {1}{33}}-\cdots \right)"/></span></dd></dl>
<p>위 식은 <a href="/wiki/%EA%B3%A0%ED%8A%B8%ED%94%84%EB%A6%AC%ED%8A%B8_%EB%B9%8C%ED%97%AC%EB%A6%84_%EB%9D%BC%EC%9D%B4%ED%94%84%EB%8B%88%EC%B8%A0" title="고트프리트 빌헬름 라이프니츠">고트프리트 빌헬름 라이프니츠</a>가 전개한 것으로 흔히 <a href="/wiki/%EB%9D%BC%EC%9D%B4%ED%94%84%EB%8B%88%EC%B8%A0%EC%9D%98_%EC%9B%90%EC%A3%BC%EC%9C%A8_%EA%B3%B5%EC%8B%9D" title="라이프니츠의 원주율 공식">라이프니츠의 공식</a>이라고 부른다. 이 식 외에도 원주율을 계산하는 공식으로는 다음과 같은 것이 있다.<sup id="cite_ref-36" class="reference"><a href="#cite_note-36">[32]</a></sup>
</p>
<dl><dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle {\frac {\pi }{2}}={\frac {2}{1}}\cdot {\frac {2}{3}}\cdot {\frac {4}{3}}\cdot {\frac {4}{5}}\cdot {\frac {6}{5}}\cdot {\frac {6}{7}}\cdot {\frac {8}{7}}\cdot {\frac {8}{9}}\cdots =\prod _{n=1}^{\infty }\left({\frac {4\cdot n^{2}}{4\cdot n^{2}-1}}\right)}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mi>π<!-- π --></mi>
<mn>2</mn>
</mfrac>
</mrow>
<mo>=</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>2</mn>
<mn>1</mn>
</mfrac>
</mrow>
<mo>⋅<!-- ⋅ --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>2</mn>
<mn>3</mn>
</mfrac>
</mrow>
<mo>⋅<!-- ⋅ --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>4</mn>
<mn>3</mn>
</mfrac>
</mrow>
<mo>⋅<!-- ⋅ --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>4</mn>
<mn>5</mn>
</mfrac>
</mrow>
<mo>⋅<!-- ⋅ --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>6</mn>
<mn>5</mn>
</mfrac>
</mrow>
<mo>⋅<!-- ⋅ --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>6</mn>
<mn>7</mn>
</mfrac>
</mrow>
<mo>⋅<!-- ⋅ --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>8</mn>
<mn>7</mn>
</mfrac>
</mrow>
<mo>⋅<!-- ⋅ --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>8</mn>
<mn>9</mn>
</mfrac>
</mrow>
<mo>⋯<!-- ⋯ --></mo>
<mo>=</mo>
<munderover>
<mo>∏<!-- ∏ --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mi>n</mi>
<mo>=</mo>
<mn>1</mn>
</mrow>
<mrow class="MJX-TeXAtom-ORD">
<mi mathvariant="normal">∞<!-- ∞ --></mi>
</mrow>
</munderover>
<mrow>
<mo>(</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mrow>
<mn>4</mn>
<mo>⋅<!-- ⋅ --></mo>
<msup>
<mi>n</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
</mrow>
<mrow>
<mn>4</mn>
<mo>⋅<!-- ⋅ --></mo>
<msup>
<mi>n</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
<mo>−<!-- − --></mo>
<mn>1</mn>
</mrow>
</mfrac>
</mrow>
<mo>)</mo>
</mrow>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle {\frac {\pi }{2}}={\frac {2}{1}}\cdot {\frac {2}{3}}\cdot {\frac {4}{3}}\cdot {\frac {4}{5}}\cdot {\frac {6}{5}}\cdot {\frac {6}{7}}\cdot {\frac {8}{7}}\cdot {\frac {8}{9}}\cdots =\prod _{n=1}^{\infty }\left({\frac {4\cdot n^{2}}{4\cdot n^{2}-1}}\right)}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/517c90971102a0acbc31db81decc3b060e50dd49" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -3.005ex; width:56.242ex; height:6.843ex;" alt="{\displaystyle {\frac {\pi }{2}}={\frac {2}{1}}\cdot {\frac {2}{3}}\cdot {\frac {4}{3}}\cdot {\frac {4}{5}}\cdot {\frac {6}{5}}\cdot {\frac {6}{7}}\cdot {\frac {8}{7}}\cdot {\frac {8}{9}}\cdots =\prod _{n=1}^{\infty }\left({\frac {4\cdot n^{2}}{4\cdot n^{2}-1}}\right)}"/></span> …… <a href="/wiki/%EC%9B%94%EB%A6%AC%EC%8A%A4_%EA%B3%B5%EC%8B%9D" title="월리스 공식">월리스 공식</a> <a href="/wiki/1655%EB%85%84" title="1655년">1655년</a></dd>
<dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle {\frac {\pi ^{2}}{6}}={\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{4^{2}}}+{\frac {1}{5^{2}}}+{\frac {1}{6^{2}}}+{\frac {1}{7^{2}}}+{\frac {1}{8^{2}}}+{\frac {1}{9^{2}}}+\cdots }">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<msup>
<mi>π<!-- π --></mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
<mn>6</mn>
</mfrac>
</mrow>
<mo>=</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<msup>
<mn>1</mn>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
</mfrac>
</mrow>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<msup>
<mn>2</mn>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
</mfrac>
</mrow>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<msup>
<mn>3</mn>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
</mfrac>
</mrow>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<msup>
<mn>4</mn>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
</mfrac>
</mrow>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<msup>
<mn>5</mn>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
</mfrac>
</mrow>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<msup>
<mn>6</mn>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
</mfrac>
</mrow>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<msup>
<mn>7</mn>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
</mfrac>
</mrow>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<msup>
<mn>8</mn>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
</mfrac>
</mrow>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<msup>
<mn>9</mn>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
</mfrac>
</mrow>
<mo>+</mo>
<mo>⋯<!-- ⋯ --></mo>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle {\frac {\pi ^{2}}{6}}={\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{4^{2}}}+{\frac {1}{5^{2}}}+{\frac {1}{6^{2}}}+{\frac {1}{7^{2}}}+{\frac {1}{8^{2}}}+{\frac {1}{9^{2}}}+\cdots }</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/fc8636762da927b84764dc7a2b412dae799d67d0" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -2.338ex; width:62.085ex; height:6.176ex;" alt="{\frac {\pi ^{2}}{6}}={\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{4^{2}}}+{\frac {1}{5^{2}}}+{\frac {1}{6^{2}}}+{\frac {1}{7^{2}}}+{\frac {1}{8^{2}}}+{\frac {1}{9^{2}}}+\cdots "/></span> ……<a href="/wiki/%EC%98%A4%EC%9D%BC%EB%9F%AC%EC%9D%98_%EA%B3%B1%EC%85%88_%EA%B3%B5%EC%8B%9D" title="오일러의 곱셈 공식">오일러의 곱셈 공식</a> <a href="/wiki/1735%EB%85%84" title="1735년">1735년</a><sup id="cite_ref-37" class="reference"><a href="#cite_note-37">[주해 5]</a></sup></dd></dl>
<p><a href="/wiki/17%EC%84%B8%EA%B8%B0" title="17세기">17세기</a>의 프랑스 수학자 <a href="/wiki/%ED%94%84%EB%9E%91%EC%88%98%EC%95%84_%EB%B9%84%EC%97%90%ED%8A%B8" title="프랑수아 비에트">프랑수아 비에트</a>는 다음과 같은 무한급수로 원주율을 계산하였다.<sup id="cite_ref-38" class="reference"><a href="#cite_note-38">[33]</a></sup><sup id="cite_ref-39" class="reference"><a href="#cite_note-39">[34]</a></sup>
</p>
<dl><dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle {\frac {\sqrt {2}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2}}}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}{2}}\cdots ={\frac {2}{\pi }}}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<msqrt>
<mn>2</mn>
</msqrt>
<mn>2</mn>
</mfrac>
</mrow>
<mo>⋅<!-- ⋅ --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<msqrt>
<mn>2</mn>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<msqrt>
<mn>2</mn>
</msqrt>
</mrow>
</msqrt>
<mn>2</mn>
</mfrac>
</mrow>
<mo>⋅<!-- ⋅ --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<msqrt>
<mn>2</mn>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<msqrt>
<mn>2</mn>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<msqrt>
<mn>2</mn>
</msqrt>
</mrow>
</msqrt>
</mrow>
</msqrt>
<mn>2</mn>
</mfrac>
</mrow>
<mo>⋯<!-- ⋯ --></mo>
<mo>=</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>2</mn>
<mi>π<!-- π --></mi>
</mfrac>
</mrow>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle {\frac {\sqrt {2}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2}}}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}{2}}\cdots ={\frac {2}{\pi }}}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/60192beddbc79dd62f37a3109fb0cad314017c0d" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -1.838ex; width:42.518ex; height:9.009ex;" alt="{\frac {{\sqrt {2}}}{2}}\cdot {\frac {{\sqrt {2+{\sqrt {2}}}}}{2}}\cdot {\frac {{\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}}{2}}\cdots ={\frac {2}{\pi }}"/></span></dd></dl>
<p>또한, <a href="/wiki/%EC%8A%A4%ED%84%B8%EB%A7%81_%EA%B7%BC%EC%82%AC" title="스털링 근사">스털링 근사</a>를 사용해 원주율을 유도할 수도 있다.<sup id="cite_ref-40" class="reference"><a href="#cite_note-40">[35]</a></sup>
</p>
<dl><dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle n!\approx {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>n</mi>
<mo>!</mo>
<mo>≈<!-- ≈ --></mo>
<mrow class="MJX-TeXAtom-ORD">
<msqrt>
<mn>2</mn>
<mi>π<!-- π --></mi>
<mi>n</mi>
</msqrt>
</mrow>
<msup>
<mrow>
<mo>(</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mi>n</mi>
<mi>e</mi>
</mfrac>
</mrow>
<mo>)</mo>
</mrow>
<mrow class="MJX-TeXAtom-ORD">
<mi>n</mi>
</mrow>
</msup>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle n!\approx {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/b7136fede6a5ec27a99e73f47a17234df0f4bd94" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -1.838ex; width:17.19ex; height:4.843ex;" alt="n!\approx {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}"/></span></dd></dl>
<p>원주율은 다음과 같이 <a href="/wiki/%EC%97%B0%EB%B6%84%EC%88%98" title="연분수">연분수</a>로 표현할 수 있다.<sup id="cite_ref-41" class="reference"><a href="#cite_note-41">[36]</a></sup>
</p>
<dl><dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle {\frac {4}{\pi }}=1+{\cfrac {1}{3+{\cfrac {4}{5+{\cfrac {9}{7+{\cfrac {16}{9+{\cfrac {25}{11+{\cfrac {36}{13+\ddots }}}}}}}}}}}}}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>4</mn>
<mi>π<!-- π --></mi>
</mfrac>
</mrow>
<mo>=</mo>
<mn>1</mn>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mrow>
<mpadded width="0" height="8.6pt" depth="3pt">
<mrow />
</mpadded>
<mstyle displaystyle="false" scriptlevel="0">
<mrow class="MJX-TeXAtom-ORD">
<mn>1</mn>
</mrow>
</mstyle>
</mrow>
<mrow>
<mpadded width="0" height="8.6pt" depth="3pt">
<mrow />
</mpadded>
<mstyle displaystyle="false" scriptlevel="0">
<mrow class="MJX-TeXAtom-ORD">
<mn>3</mn>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mrow>
<mpadded width="0" height="8.6pt" depth="3pt">
<mrow />
</mpadded>
<mstyle displaystyle="false" scriptlevel="0">
<mrow class="MJX-TeXAtom-ORD">
<mn>4</mn>
</mrow>
</mstyle>
</mrow>
<mrow>
<mpadded width="0" height="8.6pt" depth="3pt">
<mrow />
</mpadded>
<mstyle displaystyle="false" scriptlevel="0">
<mrow class="MJX-TeXAtom-ORD">
<mn>5</mn>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mrow>
<mpadded width="0" height="8.6pt" depth="3pt">
<mrow />
</mpadded>
<mstyle displaystyle="false" scriptlevel="0">
<mrow class="MJX-TeXAtom-ORD">
<mn>9</mn>
</mrow>
</mstyle>
</mrow>
<mrow>
<mpadded width="0" height="8.6pt" depth="3pt">
<mrow />
</mpadded>
<mstyle displaystyle="false" scriptlevel="0">
<mrow class="MJX-TeXAtom-ORD">
<mn>7</mn>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mrow>
<mpadded width="0" height="8.6pt" depth="3pt">
<mrow />
</mpadded>
<mstyle displaystyle="false" scriptlevel="0">
<mrow class="MJX-TeXAtom-ORD">
<mn>16</mn>
</mrow>
</mstyle>
</mrow>
<mrow>
<mpadded width="0" height="8.6pt" depth="3pt">
<mrow />
</mpadded>
<mstyle displaystyle="false" scriptlevel="0">
<mrow class="MJX-TeXAtom-ORD">
<mn>9</mn>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mrow>
<mpadded width="0" height="8.6pt" depth="3pt">
<mrow />
</mpadded>
<mstyle displaystyle="false" scriptlevel="0">
<mrow class="MJX-TeXAtom-ORD">
<mn>25</mn>
</mrow>
</mstyle>
</mrow>
<mrow>
<mpadded width="0" height="8.6pt" depth="3pt">
<mrow />
</mpadded>
<mstyle displaystyle="false" scriptlevel="0">
<mrow class="MJX-TeXAtom-ORD">
<mn>11</mn>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mrow>
<mpadded width="0" height="8.6pt" depth="3pt">
<mrow />
</mpadded>
<mstyle displaystyle="false" scriptlevel="0">
<mrow class="MJX-TeXAtom-ORD">
<mn>36</mn>
</mrow>
</mstyle>
</mrow>
<mrow>
<mpadded width="0" height="8.6pt" depth="3pt">
<mrow />
</mpadded>
<mstyle displaystyle="false" scriptlevel="0">
<mrow class="MJX-TeXAtom-ORD">
<mn>13</mn>
<mo>+</mo>
<mo>⋱<!-- ⋱ --></mo>
</mrow>
</mstyle>
</mrow>
</mfrac>
</mrow>
</mrow>
</mstyle>
</mrow>
</mfrac>
</mrow>
</mrow>
</mstyle>
</mrow>
</mfrac>
</mrow>
</mrow>
</mstyle>
</mrow>
</mfrac>
</mrow>
</mrow>
</mstyle>
</mrow>
</mfrac>
</mrow>
</mrow>
</mstyle>
</mrow>
</mfrac>
</mrow>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle {\frac {4}{\pi }}=1+{\cfrac {1}{3+{\cfrac {4}{5+{\cfrac {9}{7+{\cfrac {16}{9+{\cfrac {25}{11+{\cfrac {36}{13+\ddots }}}}}}}}}}}}}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/195d152629cb6eab8afa14e02873e2232bd4cfde" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -22.505ex; width:43.607ex; height:26.676ex;" alt="{\frac {4}{\pi }}=1+{\cfrac {1}{3+{\cfrac {4}{5+{\cfrac {9}{7+{\cfrac {16}{9+{\cfrac {25}{11+{\cfrac {36}{13+\ddots }}}}}}}}}}}}"/></span></dd></dl>
<p><a href="/wiki/1996%EB%85%84" title="1996년">1996년</a> 데이빗 베일리는 피터 보어와인, 시몽 플루프와 공동으로 π에 관련된 새로운 무한급수를 발견했다.
</p>
<dl><dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \pi =\sum _{k=0}^{\infty }{\frac {1}{16^{k}}}\left({\frac {4}{8k+1}}-{\frac {2}{8k+4}}-{\frac {1}{8k+5}}-{\frac {1}{8k+6}}\right)}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>π<!-- π --></mi>
<mo>=</mo>
<munderover>
<mo>∑<!-- ∑ --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mi>k</mi>
<mo>=</mo>
<mn>0</mn>
</mrow>
<mrow class="MJX-TeXAtom-ORD">
<mi mathvariant="normal">∞<!-- ∞ --></mi>
</mrow>
</munderover>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<msup>
<mn>16</mn>
<mrow class="MJX-TeXAtom-ORD">
<mi>k</mi>
</mrow>
</msup>
</mfrac>
</mrow>
<mrow>
<mo>(</mo>
<mrow>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>4</mn>
<mrow>
<mn>8</mn>
<mi>k</mi>
<mo>+</mo>
<mn>1</mn>
</mrow>
</mfrac>
</mrow>
<mo>−<!-- − --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>2</mn>
<mrow>
<mn>8</mn>
<mi>k</mi>
<mo>+</mo>
<mn>4</mn>
</mrow>
</mfrac>
</mrow>
<mo>−<!-- − --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mrow>
<mn>8</mn>
<mi>k</mi>
<mo>+</mo>
<mn>5</mn>
</mrow>
</mfrac>
</mrow>
<mo>−<!-- − --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mrow>
<mn>8</mn>
<mi>k</mi>
<mo>+</mo>
<mn>6</mn>
</mrow>
</mfrac>
</mrow>
</mrow>
<mo>)</mo>
</mrow>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle \pi =\sum _{k=0}^{\infty }{\frac {1}{16^{k}}}\left({\frac {4}{8k+1}}-{\frac {2}{8k+4}}-{\frac {1}{8k+5}}-{\frac {1}{8k+6}}\right)}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/5be33d7e24e7ab4d284dd957955227fb6faee2d3" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -3.171ex; width:53.602ex; height:7.009ex;" alt="\pi =\sum _{{k=0}}^{{\infty }}{\frac {1}{16^{k}}}\left({\frac {4}{8k+1}}-{\frac {2}{8k+4}}-{\frac {1}{8k+5}}-{\frac {1}{8k+6}}\right)"/></span></dd></dl>
<p>이 식을 이용하면 <a href="/wiki/2%EC%A7%84%EC%88%98" class="mw-redirect" title="2진수">2진수</a> 그리고 <a href="/wiki/16%EC%A7%84%EC%88%98" class="mw-redirect" title="16진수">16진수</a>로 표기한 π값의 소수점 아래 <i>n</i>자리 값을 <i>n</i>-1째 자리까지 구하지 않고 바로 계산해 낼 수 있다. <a rel="nofollow" class="external text" href="https://web.archive.org/web/20030501201647/http://www.nersc.gov/~dhbailey/">베일리의 홈페이지</a> 에선 다양한 <a href="/wiki/%ED%94%84%EB%A1%9C%EA%B7%B8%EB%9E%98%EB%B0%8D_%EC%96%B8%EC%96%B4" title="프로그래밍 언어">프로그래밍 언어</a>를 이용해 구현한 실제 예를 볼 수 있다.
</p>
<h2><span id=".EC.A0.81.EC.9A.A9"></span><span class="mw-headline" id="적용">적용</span><span class="mw-editsection"><span class="mw-editsection-bracket">[</span><a href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8&action=edit&section=11" title="부분 편집: 적용">편집</a><span class="mw-editsection-bracket">]</span></span></h2>
<p>원주율은 <a href="/wiki/%EC%88%98%ED%95%99" title="수학">수학</a>과 <a href="/wiki/%EB%AC%BC%EB%A6%AC%ED%95%99" title="물리학">물리학</a> 등 여러 분야에서 다양하게 적용한다.
</p>
<h3><span id=".EA.B8.B0.ED.95.98.ED.95.99"></span><span class="mw-headline" id="기하학">기하학</span><span class="mw-editsection"><span class="mw-editsection-bracket">[</span><a href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8&action=edit&section=12" title="부분 편집: 기하학">편집</a><span class="mw-editsection-bracket">]</span></span></h3>
<p><a href="/wiki/%EC%95%84%EB%A5%B4%ED%82%A4%EB%A9%94%EB%8D%B0%EC%8A%A4" title="아르키메데스">아르키메데스</a>는 <a href="/wiki/%EC%9B%90_(%EA%B8%B0%ED%95%98%ED%95%99)" title="원 (기하학)">원</a>과 <a href="/wiki/%EA%B5%AC_(%EA%B8%B0%ED%95%98%ED%95%99)" title="구 (기하학)">구</a>의 다음과 같은 성질을 증명하였다.<sup id="cite_ref-42" class="reference"><a href="#cite_note-42">[37]</a></sup>
</p>
<ul><li>반지름 <i>r</i> 인 원의 <a href="/wiki/%EB%91%98%EB%A0%88" title="둘레">둘레</a>:<span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle C=2\pi r}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>C</mi>
<mo>=</mo>
<mn>2</mn>
<mi>π<!-- π --></mi>
<mi>r</mi>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle C=2\pi r}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/398305eb631c365e21449ec4e9c9d7dca3f8c788" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.338ex; width:8.408ex; height:2.176ex;" alt="C=2\pi r"/></span></li>
<li>반지름 <i>r</i> 인 원의 <a href="/wiki/%EB%84%93%EC%9D%B4" title="넓이">넓이</a>:<span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle A=\pi r^{2}}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>A</mi>
<mo>=</mo>
<mi>π<!-- π --></mi>
<msup>
<mi>r</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle A=\pi r^{2}}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/33f7b7f93f93e7ba7bebb97efbe88e181ce332e4" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.338ex; width:8.276ex; height:2.676ex;" alt="A=\pi r^{2}"/></span></li>
<li>반지름 <i>r</i> 인 구의 <a href="/wiki/%EB%B6%80%ED%94%BC" title="부피">부피</a>:<span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle V={\frac {4}{3}}\pi r^{3}}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>V</mi>
<mo>=</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>4</mn>
<mn>3</mn>
</mfrac>
</mrow>
<mi>π<!-- π --></mi>
<msup>
<mi>r</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>3</mn>
</mrow>
</msup>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle V={\frac {4}{3}}\pi r^{3}}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/07808adf2ca4b2aeb69b6c15fb6251a3a3617c91" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -1.838ex; width:10.319ex; height:5.176ex;" alt="V={\frac {4}{3}}\pi r^{3}"/></span></li>
<li>반지름 <i>r</i> 인 구의 <a href="/wiki/%EA%B2%89%EB%84%93%EC%9D%B4" title="겉넓이">겉넓이</a>:<span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle A=4\pi r^{2}}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>A</mi>
<mo>=</mo>
<mn>4</mn>
<mi>π<!-- π --></mi>
<msup>
<mi>r</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle A=4\pi r^{2}}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/ca925588619ce34da35b2c2ffb5b267e313d50ba" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.338ex; width:9.439ex; height:2.676ex;" alt="A=4\pi r^{2}"/></span></li></ul>
<p>한편, 원은 <a href="/wiki/%EC%9D%B4%EC%8B%AC%EB%A5%A0" title="이심률">이심률</a>이 0인 <a href="/wiki/%ED%83%80%EC%9B%90" title="타원">타원</a>으로 간주할 수 있으며 이에 따라 타원 방정식은 일반적으로 다음과 같이 표현한다.<sup id="cite_ref-박은순_43-0" class="reference"><a href="#cite_note-박은순-43">[38]</a></sup><span class="reference plainlinksneverexpand" style="white-space:nowrap"><sup>:70</sup></span>
</p>
<dl><dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<msup>
<mi>x</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
<msup>
<mi>a</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
</mfrac>
</mrow>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<msup>
<mi>y</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
<msup>
<mi>b</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
</mfrac>
</mrow>
<mo>=</mo>
<mn>1</mn>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/3d7eb067b1ac196e718e5003ed60a0ea37577483" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -2.171ex; width:13.372ex; height:6.009ex;" alt="{\frac {x^{{2}}}{a^{{2}}}}+{\frac {y^{{2}}}{b^{{2}}}}=1"/></span></dd></dl>
<p>이 때 타원의 넓이를 A라 하면 다음과 같이 계산할 수 있다.
</p>
<dl><dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle A=\pi ab}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>A</mi>
<mo>=</mo>
<mi>π<!-- π --></mi>
<mi>a</mi>
<mi>b</mi>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle A=\pi ab}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/fd397a3a2665e85628460242eb4dc5d8ba0ef25d" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.338ex; width:8.401ex; height:2.176ex;" alt="A=\pi ab"/></span></dd></dl>
<div class="thumb tright"><div class="thumbinner" style="width:222px;"><a href="/wiki/%ED%8C%8C%EC%9D%BC:Angle_radian.svg" class="image"><img alt="" src="//upload.wikimedia.org/wikipedia/commons/thumb/1/15/Angle_radian.svg/220px-Angle_radian.svg.png" decoding="async" width="220" height="213" class="thumbimage" srcset="//upload.wikimedia.org/wikipedia/commons/thumb/1/15/Angle_radian.svg/330px-Angle_radian.svg.png 1.5x, //upload.wikimedia.org/wikipedia/commons/thumb/1/15/Angle_radian.svg/440px-Angle_radian.svg.png 2x" data-file-width="800" data-file-height="773" /></a> <div class="thumbcaption"><div class="magnify"><a href="/wiki/%ED%8C%8C%EC%9D%BC:Angle_radian.svg" class="internal" title="실제 크기로"></a></div>라디안의 정의</div></div></div>
<p>각의 크기를 나타내는 무차원 단위인 <a href="/wiki/%EB%9D%BC%EB%94%94%EC%95%88" title="라디안">라디안</a>은 오른쪽 그림과 같이 정의하여 반지름과 <a href="/wiki/%ED%98%B8_(%EA%B8%B0%ED%95%98%ED%95%99)" title="호 (기하학)">호</a>의 길이가 같을 때 1라디안이 된다. 따라서, 원 전체는 2π라디안이고 이를 <a href="/wiki/%EB%8F%84_(%EA%B0%81%EB%8F%84)" title="도 (각도)">도</a>로 환산하면 다음과 같다.<sup id="cite_ref-박은순_43-1" class="reference"><a href="#cite_note-박은순-43">[38]</a></sup><span class="reference plainlinksneverexpand" style="white-space:nowrap"><sup>:119</sup></span>
</p>
<ul><li>π<a href="/wiki/%EB%9D%BC%EB%94%94%EC%95%88" title="라디안">라디안</a> = 180°</li></ul>
<h3><span id=".EB.B0.94.EC.A0.A4_.EB.AC.B8.EC.A0.9C"></span><span class="mw-headline" id="바젤_문제">바젤 문제</span><span class="mw-editsection"><span class="mw-editsection-bracket">[</span><a href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8&action=edit&section=13" title="부분 편집: 바젤 문제">편집</a><span class="mw-editsection-bracket">]</span></span></h3>
<p>1687년 <a href="/wiki/%EC%8A%A4%EC%9C%84%EC%8A%A4" title="스위스">스위스</a>의 <a href="/wiki/%EB%B0%94%EC%A0%A4" title="바젤">바젤</a>의 수학 교수였던 <a href="/wiki/%EC%95%BC%EC%BD%94%ED%94%84_%EB%B2%A0%EB%A5%B4%EB%88%84%EC%9D%B4" title="야코프 베르누이">야코프 베르누이</a>와 <a href="/wiki/%EC%9A%94%ED%95%9C_%EB%B2%A0%EB%A5%B4%EB%88%84%EC%9D%B4" title="요한 베르누이">요한 베르누이</a> 형제는 <a href="/wiki/%EC%A1%B0%ED%99%94%EA%B8%89%EC%88%98" title="조화급수">조화급수</a>가 <a href="/wiki/%ED%95%A8%EC%88%98%EC%9D%98_%EA%B7%B9%ED%95%9C#발산" title="함수의 극한">발산</a>한다는 사실을 증명하였다. 그러나, 조화급수의 각 분모를 제곱한 다음 식을 닫힌 형식으로 나타내는 것에는 실패하였으며 논문의 끝에 이 문제를 해결하였다면 알려주기 바란다고 적었다.
</p>
<dl><dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle {\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{4^{2}}}+\cdots }">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<msup>
<mn>1</mn>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
</mfrac>
</mrow>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<msup>
<mn>2</mn>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
</mfrac>
</mrow>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<msup>
<mn>3</mn>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
</mfrac>
</mrow>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<msup>
<mn>4</mn>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
</mfrac>
</mrow>
<mo>+</mo>
<mo>⋯<!-- ⋯ --></mo>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle {\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{4^{2}}}+\cdots }</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/18bd3e16f388e1a3dfb61be7efadde286f78ff8f" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -2.338ex; width:26.296ex; height:5.676ex;" alt="{\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{4^{2}}}+\cdots "/></span></dd></dl>
<p>당대의 유명한 수학자들이 이 문제를 풀기 위해 시도하였으나 결국 실패하였고, 이 문제는 <a href="/wiki/%EB%B0%94%EC%A0%A4_%EB%AC%B8%EC%A0%9C" title="바젤 문제">바젤 문제</a>로 알려지며 <a href="/wiki/%ED%95%B4%EC%84%9D%ED%95%99_(%EC%88%98%ED%95%99)" title="해석학 (수학)">해석학자</a>의 악몽으로까지 불리게 되었다. 이를 해결한 사람은 <a href="/wiki/%EB%A0%88%EC%98%A8%ED%95%98%EB%A5%B4%ED%8A%B8_%EC%98%A4%EC%9D%BC%EB%9F%AC" title="레온하르트 오일러">레온하르트 오일러</a>로 1735년에 이 급수의 값이 다음과 같다는 것을 증명하였다.
</p>
<dl><dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle {\frac {\pi ^{2}}{6}}={\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{4^{2}}}+\cdots }">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<msup>
<mi>π<!-- π --></mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
<mn>6</mn>
</mfrac>
</mrow>
<mo>=</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<msup>
<mn>1</mn>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
</mfrac>
</mrow>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<msup>
<mn>2</mn>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
</mfrac>
</mrow>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<msup>
<mn>3</mn>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
</mfrac>
</mrow>
<mo>+</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<msup>
<mn>4</mn>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
</mfrac>
</mrow>
<mo>+</mo>
<mo>⋯<!-- ⋯ --></mo>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle {\frac {\pi ^{2}}{6}}={\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{4^{2}}}+\cdots }</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/edf829fbf86ae73080bce0a95c497001b8d15fb1" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -2.338ex; width:32.619ex; height:6.176ex;" alt="{\frac {\pi ^{2}}{6}}={\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{4^{2}}}+\cdots "/></span></dd></dl>
<p>후일 이 급수는 다음과 같은 일반식으로 표현되었는데 이것이 <a href="/wiki/%EB%A6%AC%EB%A7%8C_%EC%A0%9C%ED%83%80_%ED%95%A8%EC%88%98" title="리만 제타 함수">리만 제타 함수</a>이다.<sup id="cite_ref-44" class="reference"><a href="#cite_note-44">[39]</a></sup>
</p>
<dl><dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \!}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mspace width="negativethinmathspace" />
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle \!}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/78a9e37f799bdd8621f4e34e75db19fe08d108bb" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.171ex; margin-left: -0.387ex; width:0.387ex; height:0.343ex;" alt="{\displaystyle \!}"/></span></dd></dl>
<p>리만 제타 함수는 s가 짝수일 때 위 식을 이용하여 그 값을 쉽게 계산할 수 있으나 홀수일 때는 자명하지 않다. 1978년 s가 3일 때 무리수로 수렴하는 것이 증명되었다. 이 수렴값은 <a href="/wiki/%EC%95%84%ED%8E%98%EB%A6%AC_%EC%83%81%EC%88%98" title="아페리 상수">아페리 상수</a>라고 한다.<sup id="cite_ref-45" class="reference"><a href="#cite_note-45">[40]</a></sup>
</p>
<h3><span id=".EB.B3.B5.EC.86.8C.EC.88.98_.EA.B3.84.EC.82.B0"></span><span class="mw-headline" id="복소수_계산">복소수 계산</span><span class="mw-editsection"><span class="mw-editsection-bracket">[</span><a href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8&action=edit&section=14" title="부분 편집: 복소수 계산">편집</a><span class="mw-editsection-bracket">]</span></span></h3>
<div class="thumb tright"><div class="thumbinner" style="width:222px;"><a href="/wiki/%ED%8C%8C%EC%9D%BC:Euler%27s_formula.svg" class="image"><img alt="" src="//upload.wikimedia.org/wikipedia/commons/thumb/7/71/Euler%27s_formula.svg/220px-Euler%27s_formula.svg.png" decoding="async" width="220" height="236" class="thumbimage" srcset="//upload.wikimedia.org/wikipedia/commons/thumb/7/71/Euler%27s_formula.svg/330px-Euler%27s_formula.svg.png 1.5x, //upload.wikimedia.org/wikipedia/commons/thumb/7/71/Euler%27s_formula.svg/440px-Euler%27s_formula.svg.png 2x" data-file-width="512" data-file-height="549" /></a> <div class="thumbcaption"><div class="magnify"><a href="/wiki/%ED%8C%8C%EC%9D%BC:Euler%27s_formula.svg" class="internal" title="실제 크기로"></a></div><a href="/wiki/%EB%B3%B5%EC%86%8C%ED%8F%89%EB%A9%B4" title="복소평면">복소평면</a>에 그린 <a href="/wiki/%EC%98%A4%EC%9D%BC%EB%9F%AC%EC%9D%98_%EA%B3%B5%EC%8B%9D" class="mw-redirect" title="오일러의 공식">오일러의 공식</a>. 각 <i>φ</i> 가 <i>π</i> 라디안(180°)으로 증가하는 동안 오일러 등식이 성립함을 보인다.</div></div></div>
<p><a href="/wiki/%EB%B3%B5%EC%86%8C%EC%88%98" title="복소수">복소수</a> <span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle z}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>z</mi>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle z}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/bf368e72c009decd9b6686ee84a375632e11de98" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.338ex; width:1.088ex; height:1.676ex;" alt="z"/></span>는 <a href="/wiki/%EA%B7%B9%EC%A2%8C%ED%91%9C%EA%B3%84#복소수_체계" title="극좌표계">극좌표계</a>를 이용하여 다음과 같이 나타낼 수 있다.<sup id="cite_ref-46" class="reference"><a href="#cite_note-46">[41]</a></sup>
</p>
<dl><dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle z=r\cdot (\cos \varphi +i\sin \varphi )}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>z</mi>
<mo>=</mo>
<mi>r</mi>
<mo>⋅<!-- ⋅ --></mo>
<mo stretchy="false">(</mo>
<mi>cos</mi>
<mo>⁡<!-- --></mo>
<mi>φ<!-- φ --></mi>
<mo>+</mo>
<mi>i</mi>
<mi>sin</mi>
<mo>⁡<!-- --></mo>
<mi>φ<!-- φ --></mi>
<mo stretchy="false">)</mo>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle z=r\cdot (\cos \varphi +i\sin \varphi )}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/cce671667cf038ce19584f49b76737294d5be7ee" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.838ex; width:22.535ex; height:2.843ex;" alt="z=r\cdot (\cos \varphi +i\sin \varphi )"/></span></dd></dl>
<p><a href="/wiki/%EB%B3%B5%EC%86%8C%ED%95%B4%EC%84%9D%ED%95%99" title="복소해석학">복소해석학</a>에서 π는 복소수 변수가 <a href="/wiki/%EC%A7%80%EC%88%98_%ED%95%A8%EC%88%98" title="지수 함수">지수 함수</a>에서 보이는 행동과 연관이 있으며 <a href="/wiki/%EC%98%A4%EC%9D%BC%EB%9F%AC%EC%9D%98_%EA%B3%B5%EC%8B%9D" class="mw-redirect" title="오일러의 공식">오일러의 공식</a>에 따라 다음과 같이 표현할 수 있다.
</p>
<dl><dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle e^{i\varphi }=\cos \varphi +i\sin \varphi \!}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<msup>
<mi>e</mi>
<mrow class="MJX-TeXAtom-ORD">
<mi>i</mi>
<mi>φ<!-- φ --></mi>
</mrow>
</msup>
<mo>=</mo>
<mi>cos</mi>
<mo>⁡<!-- --></mo>
<mi>φ<!-- φ --></mi>
<mo>+</mo>
<mi>i</mi>
<mi>sin</mi>
<mo>⁡<!-- --></mo>
<mi>φ<!-- φ --></mi>
<mspace width="negativethinmathspace" />
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle e^{i\varphi }=\cos \varphi +i\sin \varphi \!}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/713b692e66fe16c8f55f9e6cd54f54aeb917be72" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.838ex; margin-right: -0.303ex; width:19.784ex; height:3.176ex;" alt="e^{{i\varphi }}=\cos \varphi +i\sin \varphi \!"/></span></dd></dl>
<p><i>i</i> 는 <a href="/wiki/%ED%97%88%EC%88%98_%EB%8B%A8%EC%9C%84" title="허수 단위">허수 단위</a>이기 때문에 <i>i</i><sup>2</sup> = −1 이므로 이를 π<a href="/wiki/%EB%9D%BC%EB%94%94%EC%95%88" title="라디안">라디안</a>(=180°)과 함께 <a href="/wiki/%EC%9E%90%EC%97%B0%EB%A1%9C%EA%B7%B8" title="자연로그">자연로그</a>의 밑 <a href="/wiki/E_(%EC%83%81%EC%88%98)" title="E (상수)"><i>e</i></a>의 지수로 표현하면 다음과 같은 <a href="/wiki/%EC%98%A4%EC%9D%BC%EB%9F%AC_%EB%93%B1%EC%8B%9D" class="mw-redirect" title="오일러 등식">오일러 등식</a>을 얻는다.
</p>
<dl><dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle e^{i\pi }=-1.\!}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<msup>
<mi>e</mi>
<mrow class="MJX-TeXAtom-ORD">
<mi>i</mi>
<mi>π<!-- π --></mi>
</mrow>
</msup>
<mo>=</mo>
<mo>−<!-- − --></mo>
<mn>1.</mn>
<mspace width="negativethinmathspace" />
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle e^{i\pi }=-1.\!}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/c2428a879b4a84da0ce2c0474d52fdb0c464ff39" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.505ex; margin-right: -0.204ex; width:9.357ex; height:2.843ex;" alt="e^{{i\pi }}=-1.\!"/></span></dd></dl>
<p>따라서 <i>n</i> 번째 <a href="/w/index.php?title=%EB%8B%A8%EC%9C%84%EA%B7%BC&action=edit&redlink=1" class="new" title="단위근 (없는 문서)">단위근</a>은 다음과 같다.
</p>
<dl><dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle e^{2\pi ik/n}\qquad (k=0,1,2,3,4,5,6,7,8,9\dots ,n-1)}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<msup>
<mi>e</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
<mi>π<!-- π --></mi>
<mi>i</mi>
<mi>k</mi>
<mrow class="MJX-TeXAtom-ORD">
<mo>/</mo>
</mrow>
<mi>n</mi>
</mrow>
</msup>
<mspace width="2em" />
<mo stretchy="false">(</mo>
<mi>k</mi>
<mo>=</mo>
<mn>0</mn>
<mo>,</mo>
<mn>1</mn>
<mo>,</mo>
<mn>2</mn>
<mo>,</mo>
<mn>3</mn>
<mo>,</mo>
<mn>4</mn>
<mo>,</mo>
<mn>5</mn>
<mo>,</mo>
<mn>6</mn>
<mo>,</mo>
<mn>7</mn>
<mo>,</mo>
<mn>8</mn>
<mo>,</mo>
<mn>9</mn>
<mo>…<!-- … --></mo>
<mo>,</mo>
<mi>n</mi>
<mo>−<!-- − --></mo>
<mn>1</mn>
<mo stretchy="false">)</mo>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle e^{2\pi ik/n}\qquad (k=0,1,2,3,4,5,6,7,8,9\dots ,n-1)}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e216bb5dcb0f4149660d9e089b73ea86bf05abef" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.838ex; width:47.935ex; height:3.343ex;" alt="{\displaystyle e^{2\pi ik/n}\qquad (k=0,1,2,3,4,5,6,7,8,9\dots ,n-1)}"/></span></dd></dl>
<p>이제 <a href="/wiki/%EA%B0%80%EC%9A%B0%EC%8A%A4_%EC%A0%81%EB%B6%84" title="가우스 적분">가우스 적분</a>으로 나타내면,
</p>
<dl><dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \int _{-\infty }^{\infty }e^{-x^{2}}dx={\sqrt {\pi }}}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<msubsup>
<mo>∫<!-- ∫ --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mo>−<!-- − --></mo>
<mi mathvariant="normal">∞<!-- ∞ --></mi>
</mrow>
<mrow class="MJX-TeXAtom-ORD">
<mi mathvariant="normal">∞<!-- ∞ --></mi>
</mrow>
</msubsup>
<msup>
<mi>e</mi>
<mrow class="MJX-TeXAtom-ORD">
<mo>−<!-- − --></mo>
<msup>
<mi>x</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
</mrow>
</msup>
<mi>d</mi>
<mi>x</mi>
<mo>=</mo>
<mrow class="MJX-TeXAtom-ORD">
<msqrt>
<mi>π<!-- π --></mi>
</msqrt>
</mrow>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle \int _{-\infty }^{\infty }e^{-x^{2}}dx={\sqrt {\pi }}}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e84d0d95e7b6197d827e8103191fd001382087a9" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -2.505ex; width:18.112ex; height:6.009ex;" alt="{\displaystyle \int _{-\infty }^{\infty }e^{-x^{2}}dx={\sqrt {\pi }}}"/></span></dd></dl>
<p>이 결과는 <a href="/wiki/%EB%B0%98%EC%A0%95%EC%88%98" title="반정수">반정수</a>의 <a href="/wiki/%EA%B0%90%EB%A7%88_%ED%95%A8%EC%88%98" title="감마 함수">감마 함수</a>가 √π의 유리수 곱임을 뜻한다.
</p>
<h3><span id=".ED.99.95.EB.A5.A0.EA.B3.BC_.ED.86.B5.EA.B3.84"></span><span class="mw-headline" id="확률과_통계">확률과 통계</span><span class="mw-editsection"><span class="mw-editsection-bracket">[</span><a href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8&action=edit&section=15" title="부분 편집: 확률과 통계">편집</a><span class="mw-editsection-bracket">]</span></span></h3>
<div class="thumb tright"><div class="thumbinner" style="width:222px;"><a href="/wiki/%ED%8C%8C%EC%9D%BC:Cauchy_pdf.svg" class="image"><img alt="" src="//upload.wikimedia.org/wikipedia/commons/thumb/8/8c/Cauchy_pdf.svg/220px-Cauchy_pdf.svg.png" decoding="async" width="220" height="176" class="thumbimage" srcset="//upload.wikimedia.org/wikipedia/commons/thumb/8/8c/Cauchy_pdf.svg/330px-Cauchy_pdf.svg.png 1.5x, //upload.wikimedia.org/wikipedia/commons/thumb/8/8c/Cauchy_pdf.svg/440px-Cauchy_pdf.svg.png 2x" data-file-width="360" data-file-height="288" /></a> <div class="thumbcaption"><div class="magnify"><a href="/wiki/%ED%8C%8C%EC%9D%BC:Cauchy_pdf.svg" class="internal" title="실제 크기로"></a></div><a href="/wiki/%ED%99%95%EB%A5%A0_%EB%B0%80%EB%8F%84_%ED%95%A8%EC%88%98" title="확률 밀도 함수">확률 밀도 함수</a> f(x; x_0, γ )에 대한 <a href="/w/index.php?title=%EC%BD%94%EC%8B%9C_%EB%B6%84%ED%8F%AC&action=edit&redlink=1" class="new" title="코시 분포 (없는 문서)">코시 분포</a></div></div></div>
<p><a href="/wiki/%ED%99%95%EB%A5%A0" title="확률">확률</a>과 <a href="/wiki/%ED%86%B5%EA%B3%84" title="통계">통계</a>에서 원주율이 등장하는 정리들은 다음과 같은 것들이 있다.
</p>
<ul><li><a href="/wiki/%EC%A0%95%EA%B7%9C%EB%B6%84%ED%8F%AC" class="mw-redirect" title="정규분포">정규분포</a>를 따르는 확률분포의 <a href="/wiki/%ED%8F%89%EA%B7%A0" title="평균">평균</a>을 μ, <a href="/wiki/%ED%91%9C%EC%A4%80%ED%8E%B8%EC%B0%A8" class="mw-redirect" title="표준편차">표준편차</a>를 σ라 하면, <a href="/wiki/%EA%B0%80%EC%9A%B0%EC%8A%A4_%EC%A0%81%EB%B6%84" title="가우스 적분">가우스 적분</a>의 값을 상쇄하기 위해 정규분포의 확률 밀도 함수는</li></ul>
<dl><dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle f(x)={1 \over \sigma {\sqrt {2\pi }}}\,e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>f</mi>
<mo stretchy="false">(</mo>
<mi>x</mi>
<mo stretchy="false">)</mo>
<mo>=</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mrow>
<mi>σ<!-- σ --></mi>
<mrow class="MJX-TeXAtom-ORD">
<msqrt>
<mn>2</mn>
<mi>π<!-- π --></mi>
</msqrt>
</mrow>
</mrow>
</mfrac>
</mrow>
<mspace width="thinmathspace" />
<msup>
<mi>e</mi>
<mrow class="MJX-TeXAtom-ORD">
<mo>−<!-- − --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mrow>
<mo stretchy="false">(</mo>
<mi>x</mi>
<mo>−<!-- − --></mo>
<mi>μ<!-- μ --></mi>
<msup>
<mo stretchy="false">)</mo>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
</mrow>
<mrow>
<mn>2</mn>
<msup>
<mi>σ<!-- σ --></mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
</mrow>
</mfrac>
</mrow>
</mrow>
</msup>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle f(x)={1 \over \sigma {\sqrt {2\pi }}}\,e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/46902dd8c5e71bbca525dfe9d5cc255ebebb8221" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -2.838ex; width:22.375ex; height:7.176ex;" alt="f(x)={1 \over \sigma {\sqrt {2\pi }}}\,e^{{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}}"/></span></dd></dl>
<p>이 된다.<sup id="cite_ref-47" class="reference"><a href="#cite_note-47">[42]</a></sup>
</p>
<ul><li><a href="/w/index.php?title=%EC%BD%94%EC%8B%9C_%EB%B6%84%ED%8F%AC&action=edit&redlink=1" class="new" title="코시 분포 (없는 문서)">표준 코시 분포</a>의 확률 밀도 함수:<sup id="cite_ref-48" class="reference"><a href="#cite_note-48">[43]</a></sup></li></ul>
<dl><dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle f(x)={\frac {1}{\pi (1+x^{2})}}}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>f</mi>
<mo stretchy="false">(</mo>
<mi>x</mi>
<mo stretchy="false">)</mo>
<mo>=</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mrow>
<mi>π<!-- π --></mi>
<mo stretchy="false">(</mo>
<mn>1</mn>
<mo>+</mo>
<msup>
<mi>x</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>2</mn>
</mrow>
</msup>
<mo stretchy="false">)</mo>
</mrow>
</mfrac>
</mrow>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle f(x)={\frac {1}{\pi (1+x^{2})}}}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/80c572297a929f93ce170bb9d556b375dd752308" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -2.671ex; width:17.88ex; height:6.009ex;" alt="{\displaystyle f(x)={\frac {1}{\pi (1+x^{2})}}}"/></span></dd>
<dd>참고로, 모든 확률 밀도 함수는 다음과 같이 적분한다.<sup id="cite_ref-49" class="reference"><a href="#cite_note-49">[44]</a></sup></dd>
<dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \int _{-\infty }^{\infty }f(x)\,dx=1}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<msubsup>
<mo>∫<!-- ∫ --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mo>−<!-- − --></mo>
<mi mathvariant="normal">∞<!-- ∞ --></mi>
</mrow>
<mrow class="MJX-TeXAtom-ORD">
<mi mathvariant="normal">∞<!-- ∞ --></mi>
</mrow>
</msubsup>
<mi>f</mi>
<mo stretchy="false">(</mo>
<mi>x</mi>
<mo stretchy="false">)</mo>
<mspace width="thinmathspace" />
<mi>d</mi>
<mi>x</mi>
<mo>=</mo>
<mn>1</mn>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle \int _{-\infty }^{\infty }f(x)\,dx=1}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/68613a5855dea687c5037e33f7c39b91a3ce50e5" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -2.505ex; width:16.445ex; height:6.009ex;" alt="\int _{{-\infty }}^{{\infty }}f(x)\,dx=1"/></span></dd></dl>
<p><a href="/wiki/%EC%A1%B0%EB%A5%B4%EC%A3%BC%EB%A3%A8%EC%9D%B4_%EB%A5%B4%ED%81%B4%EB%A0%88%EB%A5%B4_%EB%93%9C_%EB%B7%94%ED%90%81" class="mw-redirect" title="조르주루이 르클레르 드 뷔퐁">조르주루이 르클레르 드 뷔퐁</a>이 제기한 <a href="/wiki/%EB%B7%94%ED%90%81%EC%9D%98_%EB%B0%94%EB%8A%98" title="뷔퐁의 바늘">뷔퐁의 바늘</a> 문제는 원주율의 근삿값을 구하는 경험주의적인 방법으로 거론된다. 길이가 L인 바늘을 일정 간격으로 그린 평행선에 떨어뜨린다고 가정해 보자. 이 때 평행선의 간격 S가 바늘의 길이보다 크다고 하면, 바늘을 떨어뜨린 횟수 n번에 대해 바늘이 평행선 밖으로 나간 횟수 x번(단, x>0)에는 <a href="/wiki/%EB%AA%AC%ED%85%8C%EC%B9%B4%EB%A5%BC%EB%A1%9C_%EB%B0%A9%EB%B2%95" title="몬테카를로 방법">몬테카를로 방법</a>에 의해 다음과 같은 관계가 있다.<sup id="cite_ref-50" class="reference"><a href="#cite_note-50">[45]</a></sup>
</p>
<dl><dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \pi \approx {\frac {2nL}{xS}}.}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>π<!-- π --></mi>
<mo>≈<!-- ≈ --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mrow>
<mn>2</mn>
<mi>n</mi>
<mi>L</mi>
</mrow>
<mrow>
<mi>x</mi>
<mi>S</mi>
</mrow>
</mfrac>
</mrow>
<mo>.</mo>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle \pi \approx {\frac {2nL}{xS}}.}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/5d90a874210dd7e3589d03e4141cc532cd1885cb" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -2.005ex; width:10.053ex; height:5.343ex;" alt="\pi \approx {\frac {2nL}{xS}}."/></span></dd></dl>
<p>즉, 뷔퐁의 바늘 문제에서 바늘을 떨어뜨리는 횟수가 매우 많아지면 바늘이 평행선을 벗어나는 횟수에 대한 바늘을 떨어뜨린 전체 횟수의 비는 원주율에 근사한다.
</p>
<h3><span id=".EB.AC.BC.EB.A6.AC.ED.95.99"></span><span class="mw-headline" id="물리학">물리학</span><span class="mw-editsection"><span class="mw-editsection-bracket">[</span><a href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8&action=edit&section=16" title="부분 편집: 물리학">편집</a><span class="mw-editsection-bracket">]</span></span></h3>
<div class="thumb tright"><div class="thumbinner" style="width:222px;"><a href="/wiki/%ED%8C%8C%EC%9D%BC:Angularvelocity.svg" class="image"><img alt="" src="//upload.wikimedia.org/wikipedia/commons/thumb/d/dd/Angularvelocity.svg/220px-Angularvelocity.svg.png" decoding="async" width="220" height="190" class="thumbimage" srcset="//upload.wikimedia.org/wikipedia/commons/thumb/d/dd/Angularvelocity.svg/330px-Angularvelocity.svg.png 1.5x, //upload.wikimedia.org/wikipedia/commons/thumb/d/dd/Angularvelocity.svg/440px-Angularvelocity.svg.png 2x" data-file-width="272" data-file-height="235" /></a> <div class="thumbcaption"><div class="magnify"><a href="/wiki/%ED%8C%8C%EC%9D%BC:Angularvelocity.svg" class="internal" title="실제 크기로"></a></div>회전하는 물체에는 <a href="/wiki/%EA%B0%81%EC%86%8D%EB%8F%84" title="각속도">각속도</a>가 있다</div></div></div>
<p>원주율 자체는 <a href="/wiki/%EB%AC%BC%EB%A6%AC_%EC%83%81%EC%88%98" title="물리 상수">물리 상수</a>가 아니지만 <a href="/wiki/%EB%AC%BC%EB%A6%AC%ED%95%99" title="물리학">물리학</a>의 여러 분야에서 두루 사용한다. 이는 <a href="/wiki/%EC%9E%90%EC%97%B0" title="자연">자연</a> <a href="/wiki/%ED%98%84%EC%83%81_(%EC%B2%A0%ED%95%99)" title="현상 (철학)">현상</a>의 상당수가 <a href="/wiki/%EC%9B%90_(%EA%B8%B0%ED%95%98%ED%95%99)" title="원 (기하학)">원</a>과 관계가 있기 때문이다. 예를 들어 회전수를 일정하게 유지하는 등속원운동에서 <a href="/wiki/%EA%B0%81%EC%86%8D%EB%8F%84" title="각속도">각속도</a>와 <a href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%86%8D%EB%8F%84&action=edit&redlink=1" class="new" title="원주속도 (없는 문서)">원주속도</a>는 다음과 같이 계산할 수 있다.<sup id="cite_ref-51" class="reference"><a href="#cite_note-51">[46]</a></sup>
</p>
<dl><dd>각속도를 ω (= θ / 초), 분당 회전수를 N이라 하면</dd>
<dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \omega ={\frac {2\pi N}{60}}}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>ω<!-- ω --></mi>
<mo>=</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mrow>
<mn>2</mn>
<mi>π<!-- π --></mi>
<mi>N</mi>
</mrow>
<mn>60</mn>
</mfrac>
</mrow>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle \omega ={\frac {2\pi N}{60}}}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e2f2851df41651cf3d770587773bf201a9a10b6e" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -1.838ex; width:9.938ex; height:5.176ex;" alt="\omega ={\frac {2\pi N}{60}}"/></span></dd>
<dd>이때, 반지름을 r이라 하면 원주속도 v는</dd>
<dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle v=r\cdot \omega ={\frac {2r\pi N}{60}}}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>v</mi>
<mo>=</mo>
<mi>r</mi>
<mo>⋅<!-- ⋅ --></mo>
<mi>ω<!-- ω --></mi>
<mo>=</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mrow>
<mn>2</mn>
<mi>r</mi>
<mi>π<!-- π --></mi>
<mi>N</mi>
</mrow>
<mn>60</mn>
</mfrac>
</mrow>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle v=r\cdot \omega ={\frac {2r\pi N}{60}}}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/c75f73ecb9c06dcb897aac873c473d51dacb25e5" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -1.838ex; width:17.941ex; height:5.176ex;" alt="v=r\cdot \omega ={\frac {2r\pi N}{60}}"/></span></dd></dl>
<p>이 외에 물리학에서 원주율을 사용하는 경우는 다음과 같다.
</p>
<ul><li><a href="/wiki/%EB%B6%88%ED%99%95%EC%A0%95%EC%84%B1_%EC%9B%90%EB%A6%AC" title="불확정성 원리">불확정성 원리</a>에 따라, <a href="/wiki/%EC%96%91%EC%9E%90_%EC%97%AD%ED%95%99" class="mw-redirect" title="양자 역학">양자 역학</a>적인 <a href="/wiki/%EB%AC%BC%EB%A6%AC%EB%9F%89" title="물리량">물리량</a>은 동시에 정확히 관찰할 수 없다. 예를 들어 입자의 특정 위치를 Δ x라 하고 이 때의 <a href="/wiki/%EC%9A%B4%EB%8F%99%EB%9F%89" title="운동량">운동량</a>을 Δ p 라 하면, 이 둘의 크기를 둘 다 정확히 관찰할 수는 없으며 다음 식을 사용해 확률적으로만 계산한다.<sup id="cite_ref-52" class="reference"><a href="#cite_note-52">[47]</a></sup></li></ul>
<dl><dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \Delta x\Delta p\geq {\frac {h}{4\pi }}}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi mathvariant="normal">Δ<!-- Δ --></mi>
<mi>x</mi>
<mi mathvariant="normal">Δ<!-- Δ --></mi>
<mi>p</mi>
<mo>≥<!-- ≥ --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mi>h</mi>
<mrow>
<mn>4</mn>
<mi>π<!-- π --></mi>
</mrow>
</mfrac>
</mrow>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle \Delta x\Delta p\geq {\frac {h}{4\pi }}}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/3d590fae49786ef71895573276f343cee6129eae" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -1.838ex; width:12.8ex; height:5.343ex;" alt="\Delta x\Delta p\geq {\frac {h}{4\pi }}"/></span></dd></dl>
<ul><li><a href="/wiki/%EC%95%84%EC%9D%B8%EC%8A%88%ED%83%80%EC%9D%B8" class="mw-redirect" title="아인슈타인">아인슈타인</a>의 <a href="/wiki/%EC%9D%BC%EB%B0%98_%EC%83%81%EB%8C%80%EC%84%B1_%EC%9D%B4%EB%A1%A0" class="mw-redirect" title="일반 상대성 이론">일반 상대성 이론</a>에 의한 <a href="/wiki/%EC%95%84%EC%9D%B8%EC%8A%88%ED%83%80%EC%9D%B8_%EB%B0%A9%EC%A0%95%EC%8B%9D" title="아인슈타인 방정식">아인슈타인 방정식</a>은 다음과 같이 표현한다.<sup id="cite_ref-53" class="reference"><a href="#cite_note-53">[48]</a></sup></li></ul>
<dl><dd><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle R_{\mu \nu }-{1 \over 2}g_{\mu \nu }\,R+g_{\mu \nu }\Lambda ={8\pi G \over c^{4}}T_{\mu \nu }}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<msub>
<mi>R</mi>
<mrow class="MJX-TeXAtom-ORD">
<mi>μ<!-- μ --></mi>
<mi>ν<!-- ν --></mi>
</mrow>
</msub>
<mo>−<!-- − --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mn>1</mn>
<mn>2</mn>
</mfrac>
</mrow>
<msub>
<mi>g</mi>
<mrow class="MJX-TeXAtom-ORD">
<mi>μ<!-- μ --></mi>
<mi>ν<!-- ν --></mi>
</mrow>
</msub>
<mspace width="thinmathspace" />
<mi>R</mi>
<mo>+</mo>
<msub>
<mi>g</mi>
<mrow class="MJX-TeXAtom-ORD">
<mi>μ<!-- μ --></mi>
<mi>ν<!-- ν --></mi>
</mrow>
</msub>
<mi mathvariant="normal">Λ<!-- Λ --></mi>
<mo>=</mo>
<mrow class="MJX-TeXAtom-ORD">
<mfrac>
<mrow>
<mn>8</mn>
<mi>π<!-- π --></mi>
<mi>G</mi>
</mrow>
<msup>
<mi>c</mi>
<mrow class="MJX-TeXAtom-ORD">
<mn>4</mn>
</mrow>
</msup>
</mfrac>
</mrow>
<msub>
<mi>T</mi>
<mrow class="MJX-TeXAtom-ORD">
<mi>μ<!-- μ --></mi>
<mi>ν<!-- ν --></mi>
</mrow>
</msub>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle R_{\mu \nu }-{1 \over 2}g_{\mu \nu }\,R+g_{\mu \nu }\Lambda ={8\pi G \over c^{4}}T_{\mu \nu }}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/0641106c0b8f1e0604f6cc292c4fbc82ff318fb7" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -2.171ex; width:33.418ex; height:5.676ex;" alt="R_{{\mu \nu }}-{1 \over 2}g_{{\mu \nu }}\,R+g_{{\mu \nu }}\Lambda ={8\pi G \over c^{4}}T_{{\mu \nu }}"/></span></dd>
<dd>여기서 <span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle R_{\mu \nu }\,}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<msub>
<mi>R</mi>
<mrow class="MJX-TeXAtom-ORD">
<mi>μ<!-- μ --></mi>
<mi>ν<!-- ν --></mi>
</mrow>
</msub>
<mspace width="thinmathspace" />
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle R_{\mu \nu }\,}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/19fb5f43b5ffc8f197ecc79a16d8ac872b67ed20" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -1.005ex; width:4.246ex; height:2.843ex;" alt="R_{{\mu \nu }}\,"/></span>은 <a href="/wiki/%EB%A6%AC%EC%B9%98_%EA%B3%A1%EB%A5%A0" class="mw-redirect" title="리치 곡률">리치 곡률</a>, <span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle R\,}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>R</mi>
<mspace width="thinmathspace" />
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle R\,}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/293563891196765d2d51e0dd54e1ae1000ba9def" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.338ex; width:2.151ex; height:2.176ex;" alt="R\,"/></span> 은 <a href="/wiki/%EC%8A%A4%EC%B9%BC%EB%9D%BC_%EA%B3%A1%EB%A5%A0" title="스칼라 곡률">스칼라 곡률</a>, <span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle g_{\mu \nu }\,}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<msub>
<mi>g</mi>
<mrow class="MJX-TeXAtom-ORD">
<mi>μ<!-- μ --></mi>
<mi>ν<!-- ν --></mi>
</mrow>
</msub>
<mspace width="thinmathspace" />
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle g_{\mu \nu }\,}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/cf70b3ee2dea90750949b21cc66fbd3171f5c6b2" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -1.005ex; width:3.591ex; height:2.343ex;" alt="g_{{\mu \nu }}\,"/></span>는 <a href="/wiki/%EA%B3%84%EB%9F%89_%ED%85%90%EC%84%9C" class="mw-redirect" title="계량 텐서">계량 텐서</a>, <span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \Lambda \,}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi mathvariant="normal">Λ<!-- Λ --></mi>
<mspace width="thinmathspace" />
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle \Lambda \,}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e8ca57ff210ed95bb67bf913ce362d7e4b93810d" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.338ex; width:2ex; height:2.176ex;" alt="\Lambda \,"/></span> 는 <a href="/wiki/%EC%9A%B0%EC%A3%BC_%EC%83%81%EC%88%98" class="mw-redirect" title="우주 상수">우주 상수</a>, <span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle G\,}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>G</mi>
<mspace width="thinmathspace" />
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle G\,}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/a1f6c4d01b8be460cde4156d1fde6af720f8ff12" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.338ex; width:2.214ex; height:2.176ex;" alt="G\,"/></span> 는 <a href="/wiki/%EC%A4%91%EB%A0%A5_%EC%83%81%EC%88%98" title="중력 상수">중력 상수</a>, <span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle c\,}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>c</mi>
<mspace width="thinmathspace" />
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle c\,}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/8573e7d95140b0d4068258d8162e189563baee6b" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.338ex; width:1.394ex; height:1.676ex;" alt="c\,"/></span> 는 <a href="/wiki/%EB%B9%9B%EC%9D%98_%EC%86%8D%EB%8F%84" class="mw-redirect" title="빛의 속도">광속</a>, 그리고 <span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle T_{\mu \nu }\,}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<msub>
<mi>T</mi>
<mrow class="MJX-TeXAtom-ORD">
<mi>μ<!-- μ --></mi>
<mi>ν<!-- ν --></mi>
</mrow>
</msub>
<mspace width="thinmathspace" />
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle T_{\mu \nu }\,}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/946531a071799c2453f6e59224ac7834f566ca87" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -1.005ex; width:3.839ex; height:2.843ex;" alt="T_{{\mu \nu }}\,"/></span>는 <a href="/wiki/%EC%97%90%EB%84%88%EC%A7%80-%EC%9A%B4%EB%8F%99%EB%9F%89_%ED%85%90%EC%84%9C" title="에너지-운동량 텐서">에너지-운동량 텐서</a>이다.</dd></dl>
<h2><span id=".EA.B0.99.EC.9D.B4_.EB.B3.B4.EA.B8.B0"></span><span class="mw-headline" id="같이_보기">같이 보기</span><span class="mw-editsection"><span class="mw-editsection-bracket">[</span><a href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8&action=edit&section=17" title="부분 편집: 같이 보기">편집</a><span class="mw-editsection-bracket">]</span></span></h2>
<ul><li><a href="/wiki/%EC%9B%90%EC%A3%BC%EC%9C%A8%EC%9D%98_%EB%AC%B4%EB%A6%AC%EC%84%B1_%EC%A6%9D%EB%AA%85" title="원주율의 무리성 증명">원주율의 무리성 증명</a></li>
<li><a href="/wiki/%ED%8C%8C%EC%9D%B4%EC%9D%98_%EB%82%A0" title="파이의 날">파이의 날</a></li>
<li><a href="/wiki/%ED%8C%8C%EC%9D%B8%EB%A7%8C_%ED%8F%AC%EC%9D%B8%ED%8A%B8" title="파인만 포인트">파인만 포인트</a></li>
<li><a href="/wiki/%EB%9D%BC%EB%94%94%EC%95%88" title="라디안">라디안</a></li>
<li><a href="/wiki/%EA%B7%B8%EB%A0%88%EA%B3%A0%EB%A6%AC%EC%88%98" class="mw-redirect" title="그레고리수">그레고리 수</a></li></ul>
<h2><span id=".EC.A3.BC.ED.95.B4"></span><span class="mw-headline" id="주해">주해</span><span class="mw-editsection"><span class="mw-editsection-bracket">[</span><a href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8&action=edit&section=18" title="부분 편집: 주해">편집</a><span class="mw-editsection-bracket">]</span></span></h2>
<div class="mw-references-wrap"><ol class="references">
<li id="cite_note-28"><span class="mw-cite-backlink"><a href="#cite_ref-28">↑</a></span> <span class="reference-text"><span class="nowrap"> </span><span class="frac nowrap" lang="en"><sup>π</sup>⁄<sub>4</sub></span>는 <a href="/wiki/%EB%9D%BC%EB%94%94%EC%95%88" title="라디안">라디안</a> 값이며, <a href="/wiki/%EB%8F%84_(%EA%B0%81%EB%8F%84)" title="도 (각도)">육십분법</a>으로 나타내면 45°이다. 한편 탄젠트 함수의 값은 0일 때 0이 되며 <span class="nowrap"> </span><span class="frac nowrap" lang="en"><sup>π</sup>⁄<sub>2</sub></span>, 즉 90°일 때 무한이 된다.</span>
</li>
<li id="cite_note-30"><span class="mw-cite-backlink"><a href="#cite_ref-30">↑</a></span> <span class="reference-text"><span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle i={\sqrt {-1}}}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>i</mi>
<mo>=</mo>
<mrow class="MJX-TeXAtom-ORD">
<msqrt>
<mo>−<!-- − --></mo>
<mn>1</mn>
</msqrt>
</mrow>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle i={\sqrt {-1}}}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/370c8cebe9634fbfc84c29ea61680b0ad4a1ae0d" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.838ex; width:8.807ex; height:3.009ex;" alt="i={\sqrt {-1}}"/></span></span>
</li>
<li id="cite_note-31"><span class="mw-cite-backlink"><a href="#cite_ref-31">↑</a></span> <span class="reference-text">이와 방식이 같은 증명 가운데 <span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle {\sqrt {2}}}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mrow class="MJX-TeXAtom-ORD">
<msqrt>
<mn>2</mn>
</msqrt>
</mrow>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle {\sqrt {2}}}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/b4afc1e27d418021bf10898eb44a7f5f315735ff" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.671ex; width:3.098ex; height:3.009ex;" alt="{\sqrt {2}}"/></span>가 무리수임을 증명한 <a href="/wiki/%EC%97%90%EC%9A%B0%ED%81%B4%EB%A0%88%EC%9D%B4%EB%8D%B0%EC%8A%A4" title="에우클레이데스">에우클레이데스</a>의 증명이 널리 알려져 있다.</span>
</li>
<li id="cite_note-35"><span class="mw-cite-backlink"><a href="#cite_ref-35">↑</a></span> <span class="reference-text">배중률은 <a href="/wiki/%EB%85%BC%EB%A6%AC%ED%95%99" title="논리학">논리학</a>의 기본 공리 가운데 하나로서 A이면서 동시에 A가 아닌 경우는 없다는 것이다. <a href="/wiki/%EB%B6%88_%EB%8C%80%EC%88%98" title="불 대수">불 대수</a>로 표현하면 <span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle a\land {\neg }a=0}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>a</mi>
<mo>∧<!-- ∧ --></mo>
<mrow class="MJX-TeXAtom-ORD">
<mi mathvariant="normal">¬<!-- ¬ --></mi>
</mrow>
<mi>a</mi>
<mo>=</mo>
<mn>0</mn>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle a\land {\neg }a=0}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/043fe7cb925ea5383a17c99e69e2ab81a9529b99" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.338ex; width:10.853ex; height:2.176ex;" alt="a\land {\neg }a=0"/></span></span>
</li>
<li id="cite_note-37"><span class="mw-cite-backlink"><a href="#cite_ref-37">↑</a></span> <span class="reference-text">이 식은 <a href="/wiki/%EB%B0%94%EC%A0%A4_%EB%AC%B8%EC%A0%9C" title="바젤 문제">바젤 문제</a>의 해답으로 후일 <a href="/wiki/%EB%A6%AC%EB%A7%8C_%EC%A0%9C%ED%83%80_%ED%95%A8%EC%88%98" title="리만 제타 함수">리만 제타 함수</a>로 일반화되었을 때 <span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \zeta (2)}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>ζ<!-- ζ --></mi>
<mo stretchy="false">(</mo>
<mn>2</mn>
<mo stretchy="false">)</mo>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle \zeta (2)}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/eff246e5aba5259593186618c576a3b7e14bc3c8" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.838ex; width:4.067ex; height:2.843ex;" alt="\zeta (2)"/></span>에 해당하는 급수이다.</span>
</li>
</ol></div>
<h2><span id=".EC.B0.B8.EA.B3.A0"></span><span class="mw-headline" id="참고">참고</span><span class="mw-editsection"><span class="mw-editsection-bracket">[</span><a href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8&action=edit&section=19" title="부분 편집: 참고">편집</a><span class="mw-editsection-bracket">]</span></span></h2>
<div class="reflist columns references-column-width" style="-moz-column-width: 30em; -webkit-column-width: 30em; column-width: 30em; list-style-type: decimal;">
<ol class="references">
<li id="cite_note-1"><span class="mw-cite-backlink"><a href="#cite_ref-1">↑</a></span> <span class="reference-text">송은영, 재미있는 수학상식, 맑은창, 2007, <style data-mw-deduplicate="TemplateStyles:r23938124">.mw-parser-output cite.citation{font-style:inherit}.mw-parser-output .citation q{quotes:"\"""\"""'""'"}.mw-parser-output .citation .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-limited a,.mw-parser-output .citation .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-ws-icon a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/4/4c/Wikisource-logo.svg/12px-Wikisource-logo.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-maint{display:none;color:#33aa33;margin-left:0.3em}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em}</style><a href="/wiki/%EA%B5%AD%EC%A0%9C_%ED%91%9C%EC%A4%80_%EB%8F%84%EC%84%9C_%EB%B2%88%ED%98%B8" title="국제 표준 도서 번호">ISBN</a> <a href="/wiki/%ED%8A%B9%EC%88%98:%EC%B1%85%EC%B0%BE%EA%B8%B0/89-86607-59-X" title="특수:책찾기/89-86607-59-X">89-86607-59-X</a>, 126-133 쪽</span>
</li>
<li id="cite_note-2"><span class="mw-cite-backlink"><a href="#cite_ref-2">↑</a></span> <span class="reference-text">Pickover, Clifford A. (2005). <a rel="nofollow" class="external text" href="http://books.google.com/books?id=03CVDsZSBIcC">A passion for mathematics: numbers, puzzles, madness, religion, and the quest for reality</a>. John Wiley and Sons. p. 52. <link rel="mw-deduplicated-inline-style" href="mw-data:TemplateStyles:r23938124"/><a href="/wiki/%EA%B5%AD%EC%A0%9C_%ED%91%9C%EC%A4%80_%EB%8F%84%EC%84%9C_%EB%B2%88%ED%98%B8" title="국제 표준 도서 번호">ISBN</a> <a href="/wiki/%ED%8A%B9%EC%88%98:%EC%B1%85%EC%B0%BE%EA%B8%B0/0-471-69098-8" title="특수:책찾기/0-471-69098-8">0-471-69098-8</a>., <a rel="nofollow" class="external text" href="http://books.google.com/books?id=03CVDsZSBIcC&pg=PA52">Extract of page 52</a></span>
</li>
<li id="cite_note-사이언스타임즈-3"><span class="mw-cite-backlink">↑ <sup><a href="#cite_ref-사이언스타임즈_3-0">가</a></sup> <sup><a href="#cite_ref-사이언스타임즈_3-1">나</a></sup></span> <span class="reference-text"><a rel="nofollow" class="external text" href="http://www.sciencetimes.co.kr/article.do?todo=view&atidx=0000037014&WT.mc_id=sc_newsletter&WT.senddate=20100119&WT.linkid=0000037014">파이(π) 본격 연구는 아르키메데스부터</a> <a rel="nofollow" class="external text" href="https://web.archive.org/web/20121209175001/http://www.sciencetimes.co.kr/article.do?todo=view&atidx=0000037014&WT.mc_id=sc_newsletter&WT.senddate=20100119&WT.linkid=0000037014">Archived</a> 2012년 12월 9일 - <a href="/wiki/%EC%9B%A8%EC%9D%B4%EB%B0%B1_%EB%A8%B8%EC%8B%A0" title="웨이백 머신">웨이백 머신</a>, 사이언스타임즈, 2010년 1월 20일</span>
</li>
<li id="cite_note-4"><span class="mw-cite-backlink"><a href="#cite_ref-4">↑</a></span> <span class="reference-text"><a rel="nofollow" class="external text" href="http://mathforum.org/dr.math/faq/faq.pi.html">"About Pi"</a>. Ask Dr. Math FAQ. Retrieved 2007-10-29.</span>
</li>
<li id="cite_note-5"><span class="mw-cite-backlink"><a href="#cite_ref-5">↑</a></span> <span class="reference-text"><cite class="citation book">Stein, Sherman (2006). 《아르키메데스》. 번역 이우영. 경문사. 170쪽. <a href="/wiki/%EA%B5%AD%EC%A0%9C_%ED%91%9C%EC%A4%80_%EB%8F%84%EC%84%9C_%EB%B2%88%ED%98%B8" title="국제 표준 도서 번호">ISBN</a> <a href="/wiki/%ED%8A%B9%EC%88%98:%EC%B1%85%EC%B0%BE%EA%B8%B0/89-7282-926-9" title="특수:책찾기/89-7282-926-9"><bdi>89-7282-926-9</bdi></a>.</cite><span title="ctx_ver=Z39.88-2004&rft_val_fmt=info%3Aofi%2Ffmt%3Akev%3Amtx%3Abook&rft.genre=book&rft.btitle=%EC%95%84%EB%A5%B4%ED%82%A4%EB%A9%94%EB%8D%B0%EC%8A%A4&rft.pages=170&rft.pub=%EA%B2%BD%EB%AC%B8%EC%82%AC&rft.date=2006&rft.isbn=89-7282-926-9&rft.aulast=Stein&rft.aufirst=Sherman&rfr_id=info%3Asid%2Fko.wikipedia.org%3A%EC%9B%90%EC%A3%BC%EC%9C%A8" class="Z3988"><span style="display:none;"> </span></span></span>
</li>
<li id="cite_note-6"><span class="mw-cite-backlink"><a href="#cite_ref-6">↑</a></span> <span class="reference-text">Smith, David Eugene. <a rel="nofollow" class="external text" href="http://books.google.com/books?id=awAfO7Ff_z0C&pg=PA346&dq=%22There+are+various+other+ways+of+finding+the+Lengths+or+Areas+of+particular+Curve+Lines%22&hl=en&ei=IKT2S4L7C8L88Abv0IS9Cg&sa=X&oi=book_result&ct=result&resnum=1&ved=0CCgQ6AEwAA#v=onepage&q=%22There%20are%20various%20other%20ways%20of%20finding%20the%20Lengths%20or%20Areas%20of%20particular%20Curve%20Lines%22&f=false">A source book in mathematics</a>, Volume I, pp. 346-347.</span>
</li>
<li id="cite_note-sciencedaily.com-7"><span class="mw-cite-backlink">↑ <sup><a href="#cite_ref-sciencedaily.com_7-0">가</a></sup> <sup><a href="#cite_ref-sciencedaily.com_7-1">나</a></sup></span> <span class="reference-text"><a rel="nofollow" class="external text" href="http://www.sciencedaily.com/releases/2005/04/050427094258.htm">Pi Seems A Good Random Number Generator But Not Always The Best</a>, Science daily, 2005-4-25</span>
</li>
<li id="cite_note-Rudin-8"><span class="mw-cite-backlink"><a href="#cite_ref-Rudin_8-0">↑</a></span> <span class="reference-text"><cite class="citation book"><a href="/wiki/%EC%9B%94%ED%84%B0_%EB%A3%A8%EB%94%98" title="월터 루딘">Rudin, Walter</a> (1976). <a rel="nofollow" class="external text" href="https://web.archive.org/web/20141006165957/http://www.mcgraw-hill.com.sg/html/9780070542358.html">《Principles of mathematical analysis》</a>. International Series in Pure and Applied Mathematics (영어) 3판. McGraw-Hill. <a href="/wiki/%EA%B5%AD%EC%A0%9C_%ED%91%9C%EC%A4%80_%EB%8F%84%EC%84%9C_%EB%B2%88%ED%98%B8" title="국제 표준 도서 번호">ISBN</a> <a href="/wiki/%ED%8A%B9%EC%88%98:%EC%B1%85%EC%B0%BE%EA%B8%B0/978-0-07-054235-8" title="특수:책찾기/978-0-07-054235-8"><bdi>978-0-07-054235-8</bdi></a>. <a href="/wiki/%EC%88%98%ED%95%99_%EB%A6%AC%EB%B7%B0" title="수학 리뷰">MR</a> <a rel="nofollow" class="external text" href="//www.ams.org/mathscinet-getitem?mr=0385023">0385023</a>. <a href="/wiki/%EC%B2%B8%ED%8A%B8%EB%9E%84%EB%B8%94%EB%9D%BC%ED%8A%B8_%EB%A7%88%ED%8A%B8" title="첸트랄블라트 마트">Zbl</a> <a rel="nofollow" class="external text" href="//zbmath.org/?format=complete&q=an:0346.26002">0346.26002</a>. 2014년 10월 6일에 <a rel="nofollow" class="external text" href="http://www.mcgraw-hill.com.sg/html/9780070542358.html">원본 문서</a>에서 보존된 문서<span class="reference-accessdate">. 2014년 10월 6일에 확인함</span>.</cite><span title="ctx_ver=Z39.88-2004&rft_val_fmt=info%3Aofi%2Ffmt%3Akev%3Amtx%3Abook&rft.genre=book&rft.btitle=Principles+of+mathematical+analysis&rft.series=International+Series+in+Pure+and+Applied+Mathematics&rft.edition=3%ED%8C%90&rft.pub=McGraw-Hill&rft.date=1976&rft_id=%2F%2Fzbmath.org%2F%3Fformat%3Dcomplete%26q%3Dan%3A0346.26002&rft_id=%2F%2Fwww.ams.org%2Fmathscinet-getitem%3Fmr%3D0385023&rft.isbn=978-0-07-054235-8&rft.aulast=Rudin&rft.aufirst=Walter&rft_id=http%3A%2F%2Fwww.mcgraw-hill.com.sg%2Fhtml%2F9780070542358.html&rfr_id=info%3Asid%2Fko.wikipedia.org%3A%EC%9B%90%EC%A3%BC%EC%9C%A8" class="Z3988"><span style="display:none;"> </span></span><span class="citation-comment" style="display:none; color:#33aa33"> CS1 관리 - 추가 문구 (<a href="/wiki/%EB%B6%84%EB%A5%98:CS1_%EA%B4%80%EB%A6%AC_-_%EC%B6%94%EA%B0%80_%EB%AC%B8%EA%B5%AC" title="분류:CS1 관리 - 추가 문구">링크</a>)</span></span>
</li>
<li id="cite_note-9"><span class="mw-cite-backlink"><a href="#cite_ref-9">↑</a></span> <span class="reference-text">Beckmann, Petr (1976), A History of Pi, St. Martin's Griffin, <link rel="mw-deduplicated-inline-style" href="mw-data:TemplateStyles:r23938124"/><a href="/wiki/%EA%B5%AD%EC%A0%9C_%ED%91%9C%EC%A4%80_%EB%8F%84%EC%84%9C_%EB%B2%88%ED%98%B8" title="국제 표준 도서 번호">ISBN</a> <a href="/wiki/%ED%8A%B9%EC%88%98:%EC%B1%85%EC%B0%BE%EA%B8%B0/978-0-312-38185-1" title="특수:책찾기/978-0-312-38185-1">978-0-312-38185-1</a></span>
</li>
<li id="cite_note-김흥식-10"><span class="mw-cite-backlink">↑ <sup><a href="#cite_ref-김흥식_10-0">가</a></sup> <sup><a href="#cite_ref-김흥식_10-1">나</a></sup></span> <span class="reference-text">김흥식, 세상의 모든지식, 서해문집, 2007, <link rel="mw-deduplicated-inline-style" href="mw-data:TemplateStyles:r23938124"/><a href="/wiki/%EA%B5%AD%EC%A0%9C_%ED%91%9C%EC%A4%80_%EB%8F%84%EC%84%9C_%EB%B2%88%ED%98%B8" title="국제 표준 도서 번호">ISBN</a> <a href="/wiki/%ED%8A%B9%EC%88%98:%EC%B1%85%EC%B0%BE%EA%B8%B0/89-7483-317-4" title="특수:책찾기/89-7483-317-4">89-7483-317-4</a> 545-546쪽</span>
</li>
<li id="cite_note-11"><span class="mw-cite-backlink"><a href="#cite_ref-11">↑</a></span> <span class="reference-text">과학동아 2006년 7월호, 원주율 π의 수수께끼</span>
</li>
<li id="cite_note-12"><span class="mw-cite-backlink"><a href="#cite_ref-12">↑</a></span> <span class="reference-text">장혜원, 청소년을 위한 동양수학사, 두리미디어, 2006, <link rel="mw-deduplicated-inline-style" href="mw-data:TemplateStyles:r23938124"/><a href="/wiki/%EA%B5%AD%EC%A0%9C_%ED%91%9C%EC%A4%80_%EB%8F%84%EC%84%9C_%EB%B2%88%ED%98%B8" title="국제 표준 도서 번호">ISBN</a> <a href="/wiki/%ED%8A%B9%EC%88%98:%EC%B1%85%EC%B0%BE%EA%B8%B0/89-7715-160-0" title="특수:책찾기/89-7715-160-0">89-7715-160-0</a>, 71쪽</span>
</li>
<li id="cite_note-13"><span class="mw-cite-backlink"><a href="#cite_ref-13">↑</a></span> <span class="reference-text">나숙자, 친절한 도형 교과서, 부키, 2007, <link rel="mw-deduplicated-inline-style" href="mw-data:TemplateStyles:r23938124"/><a href="/wiki/%EA%B5%AD%EC%A0%9C_%ED%91%9C%EC%A4%80_%EB%8F%84%EC%84%9C_%EB%B2%88%ED%98%B8" title="국제 표준 도서 번호">ISBN</a> <a href="/wiki/%ED%8A%B9%EC%88%98:%EC%B1%85%EC%B0%BE%EA%B8%B0/89-6051-016-5" title="특수:책찾기/89-6051-016-5">89-6051-016-5</a>, 243쪽</span>
</li>
<li id="cite_note-14"><span class="mw-cite-backlink"><a href="#cite_ref-14">↑</a></span> <span class="reference-text">Kaye, R.W.. <a rel="nofollow" class="external text" href="http://web.mat.bham.ac.uk/R.W.Kaye/seqser/archfields">"Archimedean ordered fields"</a> <a rel="nofollow" class="external text" href="https://web.archive.org/web/20090316065753/http://web.mat.bham.ac.uk/R.W.Kaye/seqser/archfields">Archived</a> 2009년 3월 16일 - <a href="/wiki/%EC%9B%A8%EC%9D%B4%EB%B0%B1_%EB%A8%B8%EC%8B%A0" title="웨이백 머신">웨이백 머신</a>. web.mat.bham.ac.uk. Retrieved 2009-11-07.</span>
</li>
<li id="cite_note-15"><span class="mw-cite-backlink"><a href="#cite_ref-15">↑</a></span> <span class="reference-text">장혜원, 청소년을 위한 동양수학사, 두리미디어, 2006, <link rel="mw-deduplicated-inline-style" href="mw-data:TemplateStyles:r23938124"/><a href="/wiki/%EA%B5%AD%EC%A0%9C_%ED%91%9C%EC%A4%80_%EB%8F%84%EC%84%9C_%EB%B2%88%ED%98%B8" title="국제 표준 도서 번호">ISBN</a> <a href="/wiki/%ED%8A%B9%EC%88%98:%EC%B1%85%EC%B0%BE%EA%B8%B0/89-7715-160-0" title="특수:책찾기/89-7715-160-0">89-7715-160-0</a>, 70-73쪽</span>
</li>
<li id="cite_note-16"><span class="mw-cite-backlink"><a href="#cite_ref-16">↑</a></span> <span class="reference-text">위안싱페이, 장연 역, 중국문명대시야 1, 김영사, 2007, <link rel="mw-deduplicated-inline-style" href="mw-data:TemplateStyles:r23938124"/><a href="/wiki/%EA%B5%AD%EC%A0%9C_%ED%91%9C%EC%A4%80_%EB%8F%84%EC%84%9C_%EB%B2%88%ED%98%B8" title="국제 표준 도서 번호">ISBN</a> <a href="/wiki/%ED%8A%B9%EC%88%98:%EC%B1%85%EC%B0%BE%EA%B8%B0/89-349-2736-4" title="특수:책찾기/89-349-2736-4">89-349-2736-4</a>, 465쪽</span>
</li>
<li id="cite_note-17"><span class="mw-cite-backlink"><a href="#cite_ref-17">↑</a></span> <span class="reference-text">중국사학회, 강영매 역, 중국역사박물관 4, 범우사, 2004년, <link rel="mw-deduplicated-inline-style" href="mw-data:TemplateStyles:r23938124"/><a href="/wiki/%EA%B5%AD%EC%A0%9C_%ED%91%9C%EC%A4%80_%EB%8F%84%EC%84%9C_%EB%B2%88%ED%98%B8" title="국제 표준 도서 번호">ISBN</a> <a href="/wiki/%ED%8A%B9%EC%88%98:%EC%B1%85%EC%B0%BE%EA%B8%B0/89-08-04302-0" title="특수:책찾기/89-08-04302-0">89-08-04302-0</a>, 76쪽</span>
</li>
<li id="cite_note-국민일보-18"><span class="mw-cite-backlink">↑ <sup><a href="#cite_ref-국민일보_18-0">가</a></sup> <sup><a href="#cite_ref-국민일보_18-1">나</a></sup></span> <span class="reference-text"><a rel="nofollow" class="external text" href="http://news.kukinews.com/opinion/view.asp?page=4&sec=1320&arcid=0919859987&code=11171320">첨단과학과 원주율</a> <a rel="nofollow" class="external text" href="https://web.archive.org/web/20131212070634/http://news.kukinews.com/opinion/view.asp?page=4&sec=1320&arcid=0919859987&code=11171320">Archived</a> 2013년 12월 12일 - <a href="/wiki/%EC%9B%A8%EC%9D%B4%EB%B0%B1_%EB%A8%B8%EC%8B%A0" title="웨이백 머신">웨이백 머신</a>, 국민일보, 2005-7-11</span>
</li>
<li id="cite_note-사이먼-19"><span class="mw-cite-backlink">↑ <sup><a href="#cite_ref-사이먼_19-0">가</a></sup> <sup><a href="#cite_ref-사이먼_19-1">나</a></sup></span> <span class="reference-text">사이먼 싱, 박병철 역, 페르마의 마지막 정리, 영림카디널, 2002, <link rel="mw-deduplicated-inline-style" href="mw-data:TemplateStyles:r23938124"/><a href="/wiki/%EA%B5%AD%EC%A0%9C_%ED%91%9C%EC%A4%80_%EB%8F%84%EC%84%9C_%EB%B2%88%ED%98%B8" title="국제 표준 도서 번호">ISBN</a> <a href="/wiki/%ED%8A%B9%EC%88%98:%EC%B1%85%EC%B0%BE%EA%B8%B0/89-85055-97-6" title="특수:책찾기/89-85055-97-6">89-85055-97-6</a> 74-75쪽</span>
</li>
<li id="cite_note-20"><span class="mw-cite-backlink"><a href="#cite_ref-20">↑</a></span> <span class="reference-text"><a rel="nofollow" class="external text" href="http://www.jpnews.kr/sub_read.html?uid=1319&section=sc1">日, 쓰쿠바 대학 세계 신기록 원주율 자리수 계산</a>, JPNews, 2009-8-18</span>
</li>
<li id="cite_note-21"><span class="mw-cite-backlink"><a href="#cite_ref-21">↑</a></span> <span class="reference-text"><a rel="nofollow" class="external text" href="http://www.tsukuba.ac.jp/topics/20090819133359.html">円周率の計算けた数で世界記録を樹立</a>, 쓰쿠바 대학 홈페이지 (일본어)</span>
</li>
<li id="cite_note-22"><span class="mw-cite-backlink"><a href="#cite_ref-22">↑</a></span> <span class="reference-text"><a rel="nofollow" class="external text" href="http://www.sciencetimes.co.kr/article.do?todo=view&atidx=0000036918">파이(π), 2조7천억 자리까지 계산</a> <a rel="nofollow" class="external text" href="https://web.archive.org/web/20121209175021/http://www.sciencetimes.co.kr/article.do?todo=view&atidx=0000036918">Archived</a> 2012년 12월 9일 - <a href="/wiki/%EC%9B%A8%EC%9D%B4%EB%B0%B1_%EB%A8%B8%EC%8B%A0" title="웨이백 머신">웨이백 머신</a>, 사이언스타임즈, 2010-1-19</span>
</li>
<li id="cite_note-23"><span class="mw-cite-backlink"><a href="#cite_ref-23">↑</a></span> <span class="reference-text"><a rel="nofollow" class="external text" href="http://news.naver.com/main/read.nhn?mode=LSD&mid=sec&sid1=104&oid=003&aid=0003410598">日회사원, 원주율 소수점 이하 5조 자리까지 계산 성공 :: 네이버 뉴스</a></span>
</li>
<li id="cite_note-24"><span class="mw-cite-backlink"><a href="#cite_ref-24">↑</a></span> <span class="reference-text">Peter Trüb가 계산한 <span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \pi }">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>π<!-- π --></mi>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle \pi }</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/9be4ba0bb8df3af72e90a0535fabcc17431e540a" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.338ex; width:1.332ex; height:1.676ex;" alt="\pi"/></span> 값 22조 자리 중 첫 1조 자리의 값은 <a rel="nofollow" class="external free" href="http://pi2e.ch/blog/">http://pi2e.ch/blog/</a> 사이트에서 다운로드 받을 수 있다.</span>
</li>
<li id="cite_note-25"><span class="mw-cite-backlink"><a href="#cite_ref-25">↑</a></span> <span class="reference-text">김흥식, 세상의 모든지식, 서해문집, 2007, <link rel="mw-deduplicated-inline-style" href="mw-data:TemplateStyles:r23938124"/><a href="/wiki/%EA%B5%AD%EC%A0%9C_%ED%91%9C%EC%A4%80_%EB%8F%84%EC%84%9C_%EB%B2%88%ED%98%B8" title="국제 표준 도서 번호">ISBN</a> <a href="/wiki/%ED%8A%B9%EC%88%98:%EC%B1%85%EC%B0%BE%EA%B8%B0/89-7483-317-4" title="특수:책찾기/89-7483-317-4">89-7483-317-4</a> 547쪽</span>
</li>
<li id="cite_note-26"><span class="mw-cite-backlink"><a href="#cite_ref-26">↑</a></span> <span class="reference-text">Laczkovich, Miklós (1997), <a rel="nofollow" class="external text" href="http://www.jstor.org/pss/2974737">"On Lambert's proof of the irrationality of π"</a>, American Mathematical Monthly 104 (5): 439–443, ISSN 0002-9890</span>
</li>
<li id="cite_note-27"><span class="mw-cite-backlink"><a href="#cite_ref-27">↑</a></span> <span class="reference-text">Zhou, Li; Markov, Lubomir (2010), <a rel="nofollow" class="external text" href="http://arxiv.org/PS_cache/arxiv/pdf/0911/0911.1933v1.pdf">"Recurrent Proofs of the Irrationality of Certain Trigonometric Values"</a>, American Mathematical Monthly 117 (4): 360–362</span>
</li>
<li id="cite_note-29"><span class="mw-cite-backlink"><a href="#cite_ref-29">↑</a></span> <span class="reference-text">김태성, <a rel="nofollow" class="external text" href="http://www.papersearch.net/view/detail.asp?detail_key=10300189">e 및 π의 초월성과 고등학교에서 초월수 지도</a> <a rel="nofollow" class="external text" href="https://web.archive.org/web/20121107054942/http://www.papersearch.net/view/detail.asp?detail_key=10300189">Archived</a> 2012년 11월 7일 - <a href="/wiki/%EC%9B%A8%EC%9D%B4%EB%B0%B1_%EB%A8%B8%EC%8B%A0" title="웨이백 머신">웨이백 머신</a>, 한국수학교육학회 A 통권 14권 2호, 1976년, 17-22</span>
</li>
<li id="cite_note-32"><span class="mw-cite-backlink"><a href="#cite_ref-32">↑</a></span> <span class="reference-text"><a rel="nofollow" class="external text" href="http://www.mathematik.uni-muenchen.de/~fritsch/pi.pdf">Hilberts Beweis der Transzendenz der Ludolphschen Zahl π</a> <a rel="nofollow" class="external text" href="https://web.archive.org/web/20110716060726/http://www.mathematik.uni-muenchen.de/~fritsch/pi.pdf">Archived</a> 2011년 7월 16일 - <a href="/wiki/%EC%9B%A8%EC%9D%B4%EB%B0%B1_%EB%A8%B8%EC%8B%A0" title="웨이백 머신">웨이백 머신</a>(독일어)</span>
</li>
<li id="cite_note-장우석-33"><span class="mw-cite-backlink">↑ <sup><a href="#cite_ref-장우석_33-0">가</a></sup> <sup><a href="#cite_ref-장우석_33-1">나</a></sup></span> <span class="reference-text">장우석, 수학 철학에 미치다, 숨비소리, 2008년, <link rel="mw-deduplicated-inline-style" href="mw-data:TemplateStyles:r23938124"/><a href="/wiki/%EA%B5%AD%EC%A0%9C_%ED%91%9C%EC%A4%80_%EB%8F%84%EC%84%9C_%EB%B2%88%ED%98%B8" title="국제 표준 도서 번호">ISBN</a> <a href="/wiki/%ED%8A%B9%EC%88%98:%EC%B1%85%EC%B0%BE%EA%B8%B0/89-93265-01-1" title="특수:책찾기/89-93265-01-1">89-93265-01-1</a>, 174-178쪽</span>
</li>
<li id="cite_note-34"><span class="mw-cite-backlink"><a href="#cite_ref-34">↑</a></span> <span class="reference-text">Arndt, J. & Haenel, C. (2001), <a rel="nofollow" class="external text" href="http://books.google.com/books?id=JlG5rFH7Ge0C&dq=Feynman&pg=PA3">Pi — Unleashed</a>, Berlin: Springer, p. 3, <link rel="mw-deduplicated-inline-style" href="mw-data:TemplateStyles:r23938124"/><a href="/wiki/%EA%B5%AD%EC%A0%9C_%ED%91%9C%EC%A4%80_%EB%8F%84%EC%84%9C_%EB%B2%88%ED%98%B8" title="국제 표준 도서 번호">ISBN</a> <a href="/wiki/%ED%8A%B9%EC%88%98:%EC%B1%85%EC%B0%BE%EA%B8%B0/3-540-66572-2" title="특수:책찾기/3-540-66572-2">3-540-66572-2</a>.</span>
</li>
<li id="cite_note-36"><span class="mw-cite-backlink"><a href="#cite_ref-36">↑</a></span> <span class="reference-text">나카다 노리오, 황소연 역, 피라미드에서 수학을 배우자 (수학의 도레미 3), 이지북, 2001년, <link rel="mw-deduplicated-inline-style" href="mw-data:TemplateStyles:r23938124"/><a href="/wiki/%EA%B5%AD%EC%A0%9C_%ED%91%9C%EC%A4%80_%EB%8F%84%EC%84%9C_%EB%B2%88%ED%98%B8" title="국제 표준 도서 번호">ISBN</a> <a href="/wiki/%ED%8A%B9%EC%88%98:%EC%B1%85%EC%B0%BE%EA%B8%B0/89-89422-62-0" title="특수:책찾기/89-89422-62-0">89-89422-62-0</a>, 160-161쪽</span>
</li>
<li id="cite_note-38"><span class="mw-cite-backlink"><a href="#cite_ref-38">↑</a></span> <span class="reference-text">Pierre Eymard,Jean Pierre Lafon, <a rel="nofollow" class="external text" href="http://books.google.co.kr/books?id=qZcCSskdtwcC&pg=PA44&dq=viete+pi&hl=ko&ei=q5tMTa_6JcOrcc_CzfsF&sa=X&oi=book_result&ct=result&resnum=1&ved=0CCsQ6AEwAA#v=onepage&q&f=false">The number π</a>, 45p.</span>
</li>
<li id="cite_note-39"><span class="mw-cite-backlink"><a href="#cite_ref-39">↑</a></span> <span class="reference-text"><a rel="nofollow" class="external text" href="https://books.google.co.kr/books/about/Opera_mathematica_opera_atque_studio_Fra.html?id=JmBDAAAAcAAJ&redir_esc=y(P400L17,Variorum">Opera mathematica ... opera atque studio Francisci à Schooten, Leydensis, ...</a> - P400L17,Variorum de rebus Mathèmaticis Reíponíorum Liber VIII</span>
</li>
<li id="cite_note-40"><span class="mw-cite-backlink"><a href="#cite_ref-40">↑</a></span> <span class="reference-text">Lennart Berggren,Jonathan M. Borwein,Peter B. Borwein, <a rel="nofollow" class="external text" href="http://books.google.co.kr/books?id=QlbzjN_5pDoC&pg=PA412&dq=Stirling's+approximation+pi&hl=ko&ei=qZ1MTd7EEsLIcaPYse0L&sa=X&oi=book_result&ct=result&resnum=1&ved=0CCsQ6AEwAA#v=onepage&q&f=false">Pi, a source book</a></span>
</li>
<li id="cite_note-41"><span class="mw-cite-backlink"><a href="#cite_ref-41">↑</a></span> <span class="reference-text">Lange, L. J. (May 1999). <a rel="nofollow" class="external text" href="http://www.jstor.org/stable/2589152">"An Elegant Continued Fraction for π"</a>. The American Mathematical Monthly 106 (5): 456–458. doi:10.2307/2589152</span>
</li>
<li id="cite_note-42"><span class="mw-cite-backlink"><a href="#cite_ref-42">↑</a></span> <span class="reference-text"><cite class="citation book">Stein, Sherman (2006). 《아르키메데스》. 번역 이우영. 경문사. 145-168쪽. <a href="/wiki/%EA%B5%AD%EC%A0%9C_%ED%91%9C%EC%A4%80_%EB%8F%84%EC%84%9C_%EB%B2%88%ED%98%B8" title="국제 표준 도서 번호">ISBN</a> <a href="/wiki/%ED%8A%B9%EC%88%98:%EC%B1%85%EC%B0%BE%EA%B8%B0/89-7282-926-9" title="특수:책찾기/89-7282-926-9"><bdi>89-7282-926-9</bdi></a>.</cite><span title="ctx_ver=Z39.88-2004&rft_val_fmt=info%3Aofi%2Ffmt%3Akev%3Amtx%3Abook&rft.genre=book&rft.btitle=%EC%95%84%EB%A5%B4%ED%82%A4%EB%A9%94%EB%8D%B0%EC%8A%A4&rft.pages=145-168&rft.pub=%EA%B2%BD%EB%AC%B8%EC%82%AC&rft.date=2006&rft.isbn=89-7282-926-9&rft.aulast=Stein&rft.aufirst=Sherman&rfr_id=info%3Asid%2Fko.wikipedia.org%3A%EC%9B%90%EC%A3%BC%EC%9C%A8" class="Z3988"><span style="display:none;"> </span></span></span>
</li>
<li id="cite_note-박은순-43"><span class="mw-cite-backlink">↑ <sup><a href="#cite_ref-박은순_43-0">가</a></sup> <sup><a href="#cite_ref-박은순_43-1">나</a></sup></span> <span class="reference-text"><cite class="citation book">박은순 (2008). 《쉬운 미분·적분학》. 숭실대학교출판부. <a href="/wiki/%EA%B5%AD%EC%A0%9C_%ED%91%9C%EC%A4%80_%EB%8F%84%EC%84%9C_%EB%B2%88%ED%98%B8" title="국제 표준 도서 번호">ISBN</a> <a href="/wiki/%ED%8A%B9%EC%88%98:%EC%B1%85%EC%B0%BE%EA%B8%B0/89-7450-235-6" title="특수:책찾기/89-7450-235-6"><bdi>89-7450-235-6</bdi></a>.</cite><span title="ctx_ver=Z39.88-2004&rft_val_fmt=info%3Aofi%2Ffmt%3Akev%3Amtx%3Abook&rft.genre=book&rft.btitle=%EC%89%AC%EC%9A%B4+%EB%AF%B8%EB%B6%84%C2%B7%EC%A0%81%EB%B6%84%ED%95%99&rft.pub=%EC%88%AD%EC%8B%A4%EB%8C%80%ED%95%99%EA%B5%90%EC%B6%9C%ED%8C%90%EB%B6%80&rft.date=2008&rft.isbn=89-7450-235-6&rft.au=%EB%B0%95%EC%9D%80%EC%88%9C&rfr_id=info%3Asid%2Fko.wikipedia.org%3A%EC%9B%90%EC%A3%BC%EC%9C%A8" class="Z3988"><span style="display:none;"> </span></span></span>
</li>
<li id="cite_note-44"><span class="mw-cite-backlink"><a href="#cite_ref-44">↑</a></span> <span class="reference-text">존 더비셔, 박병철 역, 《리만 가설》, 승산, <link rel="mw-deduplicated-inline-style" href="mw-data:TemplateStyles:r23938124"/><a href="/wiki/%EA%B5%AD%EC%A0%9C_%ED%91%9C%EC%A4%80_%EB%8F%84%EC%84%9C_%EB%B2%88%ED%98%B8" title="국제 표준 도서 번호">ISBN</a> <a href="/wiki/%ED%8A%B9%EC%88%98:%EC%B1%85%EC%B0%BE%EA%B8%B0/978-89-88907-88-7" title="특수:책찾기/978-89-88907-88-7">978-89-88907-88-7</a>, 99-122쪽</span>
</li>
<li id="cite_note-45"><span class="mw-cite-backlink"><a href="#cite_ref-45">↑</a></span> <span class="reference-text"><a rel="nofollow" class="external text" href="http://rjlipton.wordpress.com/2010/07/11/proving-a-proof-is-a-proof/">Proving A Proof Is A Proof « Gödel’s Lost Letter and P=NP</a></span>
</li>
<li id="cite_note-46"><span class="mw-cite-backlink"><a href="#cite_ref-46">↑</a></span> <span class="reference-text">Smith, Julius O.. <a rel="nofollow" class="external text" href="https://ccrma.stanford.edu/~jos/mdft/Euler_s_Identity.html">"Euler's Identity"</a>, Mathematics of the Discrete Fourier Transform (DFT). W3K Publishing. 0-9745607-0-7. 2011년 2월 5일에 확인.</span>
</li>
<li id="cite_note-47"><span class="mw-cite-backlink"><a href="#cite_ref-47">↑</a></span> <span class="reference-text"><a rel="nofollow" class="external text" href="http://mathworld.wolfram.com/GaussianIntegral.html">Gaussian Integral</a>, MathWorld, 2004-10-07 확인</span>
</li>
<li id="cite_note-48"><span class="mw-cite-backlink"><a href="#cite_ref-48">↑</a></span> <span class="reference-text"><a rel="nofollow" class="external text" href="http://mathworld.wolfram.com/CauchyDistribution.html">Cauchy Distribution</a>, MathWorld, 2007-11-08 확인</span>
</li>
<li id="cite_note-49"><span class="mw-cite-backlink"><a href="#cite_ref-49">↑</a></span> <span class="reference-text"><a rel="nofollow" class="external text" href="http://mathworld.wolfram.com/ProbabilityFunction.html">Probability Function</a><sup class="정리_필요 noprint">[<a href="/wiki/%EC%9C%84%ED%82%A4%EB%B0%B1%EA%B3%BC:%EA%B9%A8%EC%A7%84_%EB%A7%81%ED%81%AC" title="위키백과:깨진 링크">깨진 링크</a>(<a rel="nofollow" class="external text" href="http://web.archive.org/web/*/http://mathworld.wolfram.com/ProbabilityFunction.html">과거 내용 찾기</a>)]</sup>, MathWorld, 2007-11-08 확인함</span>
</li>
<li id="cite_note-50"><span class="mw-cite-backlink"><a href="#cite_ref-50">↑</a></span> <span class="reference-text">Weisstein, Eric W (2005-12-12). <a rel="nofollow" class="external text" href="http://mathworld.wolfram.com/BuffonsNeedleProblem.html">"Buffon's Needle Problem"</a>. MathWorld. Retrieved 2007-11-10.</span>
</li>
<li id="cite_note-51"><span class="mw-cite-backlink"><a href="#cite_ref-51">↑</a></span> <span class="reference-text">문성수, 정설 재료역학, 기전연구사, 2000년, <link rel="mw-deduplicated-inline-style" href="mw-data:TemplateStyles:r23938124"/><a href="/wiki/%EA%B5%AD%EC%A0%9C_%ED%91%9C%EC%A4%80_%EB%8F%84%EC%84%9C_%EB%B2%88%ED%98%B8" title="국제 표준 도서 번호">ISBN</a> <a href="/wiki/%ED%8A%B9%EC%88%98:%EC%B1%85%EC%B0%BE%EA%B8%B0/89-336-0539-8" title="특수:책찾기/89-336-0539-8">89-336-0539-8</a>, 52-53쪽</span>
</li>
<li id="cite_note-52"><span class="mw-cite-backlink"><a href="#cite_ref-52">↑</a></span> <span class="reference-text">존 테일러, 강희재 외 역, 현대물리학, 교보문고, 2005, <link rel="mw-deduplicated-inline-style" href="mw-data:TemplateStyles:r23938124"/><a href="/wiki/%EA%B5%AD%EC%A0%9C_%ED%91%9C%EC%A4%80_%EB%8F%84%EC%84%9C_%EB%B2%88%ED%98%B8" title="국제 표준 도서 번호">ISBN</a> <a href="/wiki/%ED%8A%B9%EC%88%98:%EC%B1%85%EC%B0%BE%EA%B8%B0/89-7085-543-2" title="특수:책찾기/89-7085-543-2">89-7085-543-2</a>, 242-244쪽</span>
</li>
<li id="cite_note-53"><span class="mw-cite-backlink"><a href="#cite_ref-53">↑</a></span> <span class="reference-text">Einstein, Albert (1916). <a rel="nofollow" class="external text" href="http://www.alberteinstein.info/gallery/gtext3.html">"The Foundation of the General Theory of Relativity"</a> <a rel="nofollow" class="external text" href="https://web.archive.org/web/20060829045130/http://www.alberteinstein.info/gallery/gtext3.html">Archived</a> 2006년 8월 29일 - <a href="/wiki/%EC%9B%A8%EC%9D%B4%EB%B0%B1_%EB%A8%B8%EC%8B%A0" title="웨이백 머신">웨이백 머신</a> (PDF). Annalen der Physik.</span>
</li>
</ol></div>
<h2><span id=".EC.99.B8.EB.B6.80_.EB.A7.81.ED.81.AC"></span><span class="mw-headline" id="외부_링크">외부 링크</span><span class="mw-editsection"><span class="mw-editsection-bracket">[</span><a href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8&action=edit&section=20" title="부분 편집: 외부 링크">편집</a><span class="mw-editsection-bracket">]</span></span></h2>
<ul><li><img alt="" src="//upload.wikimedia.org/wikipedia/commons/thumb/4/4a/Commons-logo.svg/12px-Commons-logo.svg.png" decoding="async" width="12" height="16" srcset="//upload.wikimedia.org/wikipedia/commons/thumb/4/4a/Commons-logo.svg/18px-Commons-logo.svg.png 1.5x, //upload.wikimedia.org/wikipedia/commons/thumb/4/4a/Commons-logo.svg/24px-Commons-logo.svg.png 2x" data-file-width="1024" data-file-height="1376" /> 위키미디어 공용에 <span class="plainlinks"><a class="external text" href="https://commons.wikimedia.org/wiki/Category:Pi?uselang=ko">원주율</a></span> 관련 미디어 분류가 있습니다.</li>
<li><cite class="citation web"><a rel="nofollow" class="external text" href="http://navercast.naver.com/contents.nhn?contents_id=1094">“산학의 원주율”</a>. 《<a href="/wiki/%EB%84%A4%EC%9D%B4%EB%B2%84%EC%BA%90%EC%8A%A4%ED%8A%B8" title="네이버캐스트">네이버캐스트</a>》.</cite><span title="ctx_ver=Z39.88-2004&rft_val_fmt=info%3Aofi%2Ffmt%3Akev%3Amtx%3Ajournal&rft.genre=unknown&rft.jtitle=%EB%84%A4%EC%9D%B4%EB%B2%84%EC%BA%90%EC%8A%A4%ED%8A%B8&rft.atitle=%EC%82%B0%ED%95%99%EC%9D%98+%EC%9B%90%EC%A3%BC%EC%9C%A8&rft_id=http%3A%2F%2Fnavercast.naver.com%2Fcontents.nhn%3Fcontents_id%3D1094&rfr_id=info%3Asid%2Fko.wikipedia.org%3A%EC%9B%90%EC%A3%BC%EC%9C%A8" class="Z3988"><span style="display:none;"> </span></span></li>
<li><cite class="citation web"><a rel="nofollow" class="external text" href="http://navercast.naver.com/contents.nhn?contents_id=204">“원주율 π”</a>. 《<a href="/wiki/%EB%84%A4%EC%9D%B4%EB%B2%84%EC%BA%90%EC%8A%A4%ED%8A%B8" title="네이버캐스트">네이버캐스트</a>》.</cite><span title="ctx_ver=Z39.88-2004&rft_val_fmt=info%3Aofi%2Ffmt%3Akev%3Amtx%3Ajournal&rft.genre=unknown&rft.jtitle=%EB%84%A4%EC%9D%B4%EB%B2%84%EC%BA%90%EC%8A%A4%ED%8A%B8&rft.atitle=%EC%9B%90%EC%A3%BC%EC%9C%A8+%CF%80&rft_id=http%3A%2F%2Fnavercast.naver.com%2Fcontents.nhn%3Fcontents_id%3D204&rfr_id=info%3Asid%2Fko.wikipedia.org%3A%EC%9B%90%EC%A3%BC%EC%9C%A8" class="Z3988"><span style="display:none;"> </span></span></li>
<li><a rel="nofollow" class="external text" href="http://math.bab2min.pe.kr/pi">온라인 원주율 계산기</a></li>
<li><b><span style="color: #555; font-size: smaller;" title="언어: 영어">(영어)</span></b> <a rel="nofollow" class="external text" href="http://www.gutenberg.net/etext/50">Project Gutenberg E-Text containing a million digits of Pi</a></li>
<li><b><span style="color: #555; font-size: smaller;" title="언어: 영어">(영어)</span></b> <a rel="nofollow" class="external text" href="http://mathworld.wolfram.com/PiFormulas.html">From the Wolfram Mathematics site lots of formulae for π</a></li>
<li><b><span style="color: #555; font-size: smaller;" title="언어: 영어">(영어)</span></b> <a rel="nofollow" class="external text" href="http://www.angio.net/pi/bigpi.cgi">원주율에 관한 것</a></li>
<li><b><span style="color: #555; font-size: smaller;" title="언어: 영어">(영어)</span></b> <a rel="nofollow" class="external text" href="http://pi2e.ch/blog/">Peter Trüb가 계산한 원주율 - 소수점 아래 22조 자리까지 계산</a></li></ul>
<div role="navigation" class="navbox" aria-labelledby="무리수" style="padding:3px"><table class="nowraplinks mw-collapsible autocollapse navbox-inner" style="border-spacing:0;background:transparent;color:inherit"><tbody><tr><th scope="col" class="navbox-title" colspan="3"><div class="plainlinks hlist navbar mini"><ul><li class="nv-view"><a href="/wiki/%ED%8B%80:%EB%AC%B4%EB%A6%AC%EC%88%98" title="틀:무리수"><abbr title="이 틀을 보기" style=";;background:none transparent;border:none;-moz-box-shadow:none;-webkit-box-shadow:none;box-shadow:none; padding:0;">v</abbr></a></li><li class="nv-talk"><a href="/w/index.php?title=%ED%8B%80%ED%86%A0%EB%A1%A0:%EB%AC%B4%EB%A6%AC%EC%88%98&action=edit&redlink=1" class="new" title="틀토론:무리수 (없는 문서)"><abbr title="이 틀에 대한 토론" style=";;background:none transparent;border:none;-moz-box-shadow:none;-webkit-box-shadow:none;box-shadow:none; padding:0;">t</abbr></a></li><li class="nv-edit"><a class="external text" href="https://ko.wikipedia.org/w/index.php?title=%ED%8B%80:%EB%AC%B4%EB%A6%AC%EC%88%98&action=edit"><abbr title="이 틀을 편집하기" style=";;background:none transparent;border:none;-moz-box-shadow:none;-webkit-box-shadow:none;box-shadow:none; padding:0;">e</abbr></a></li></ul></div><div id="무리수" style="font-size:114%;margin:0 4em"><a href="/wiki/%EB%AC%B4%EB%A6%AC%EC%88%98" title="무리수">무리수</a></div></th></tr><tr><td colspan="2" class="navbox-list navbox-odd hlist" style="width:100%;padding:0px"><div style="padding:0em 0.25em">
<ul><li><a href="/wiki/%EC%B9%B4%EC%9D%B4%ED%8B%B4_%EC%83%81%EC%88%98" title="카이틴 상수">카이틴 상수</a> (<style data-mw-deduplicate="TemplateStyles:r25030363">.mw-parser-output .texhtml{font-family:"Nimbus Roman No9 L","Times New Roman",Times,serif;white-space:nowrap;line-height:1;font-size:118%}</style><span class="texhtml">Ω</span>)</li>
<li><a href="/wiki/%EB%A6%AC%EC%9A%B0%EB%B9%8C_%EC%88%98" title="리우빌 수">리우빌 상수</a></li>
<li>소수 상수 (<link rel="mw-deduplicated-inline-style" href="mw-data:TemplateStyles:r25030363"/><span class="texhtml" style="font-style: italic;">ρ</span>)</li>
<li>자연로그 2</li>
<li><a href="/wiki/%EA%B0%80%EC%9A%B0%EC%8A%A4_%EC%83%81%EC%88%98" title="가우스 상수">가우스 상수</a> (<link rel="mw-deduplicated-inline-style" href="mw-data:TemplateStyles:r25030363"/><span class="texhtml" style="font-style: italic;">G</span>)</li>
<li><a href="/wiki/%EC%97%B4%EB%91%90%EC%A0%9C%EA%B3%B1%EA%B7%BC_2" title="열두제곱근 2">2의 12제곱근</a> (<span class="nowrap"><sup style="margin-right: -0.5em; vertical-align: 0.8em;">12</sup>√<span style="border-top:1px solid; padding:0 0.1em;">2</span></span>)</li>
<li><a href="/wiki/%EC%95%84%ED%8E%98%EB%A6%AC_%EC%83%81%EC%88%98" title="아페리 상수">아페리</a> (<link rel="mw-deduplicated-inline-style" href="mw-data:TemplateStyles:r25030363"/><span class="texhtml"><i>ζ</i>(3)</span>)</li></ul>
<ul><li><a href="/wiki/%ED%94%8C%EB%9D%BC%EC%8A%A4%ED%8B%B1_%EC%88%98" title="플라스틱 수">플라스틱 수</a> (<link rel="mw-deduplicated-inline-style" href="mw-data:TemplateStyles:r25030363"/><span class="texhtml" style="font-style: italic;">ρ</span>)</li>
<li><a href="/wiki/%EC%A0%9C%EA%B3%B1%EA%B7%BC_2" title="제곱근 2">제곱근 2</a> (<span class="nowrap">√<span style="border-top:1px solid; padding:0 0.1em;">2</span></span>)</li>
<li><a href="/wiki/%EC%B4%88%ED%99%A9%EA%B8%88%EB%B9%84" title="초황금비">초황금비</a> (<link rel="mw-deduplicated-inline-style" href="mw-data:TemplateStyles:r25030363"/><span class="texhtml" style="font-style: italic;">ψ</span>)</li>
<li><a href="/wiki/%EC%97%90%EB%A5%B4%EB%90%98%EC%8B%9C-%EB%B3%B4%EC%96%B4%EC%99%80%EC%9D%B8_%EC%83%81%EC%88%98" title="에르되시-보어와인 상수">에르되시-보어와인</a> (<link rel="mw-deduplicated-inline-style" href="mw-data:TemplateStyles:r25030363"/><span class="texhtml" style="font-style: italic;">E</span>)</li>
<li><a href="/wiki/%ED%99%A9%EA%B8%88%EB%B9%84" title="황금비">황금비</a> (<link rel="mw-deduplicated-inline-style" href="mw-data:TemplateStyles:r25030363"/><span class="texhtml" style="font-style: italic;">φ</span>)</li>
<li><a href="/wiki/%EC%A0%9C%EA%B3%B1%EA%B7%BC_3" title="제곱근 3">제곱근 3</a> (<span class="nowrap">√<span style="border-top:1px solid; padding:0 0.1em;">3</span></span>)</li>
<li><a href="/wiki/%EC%A0%9C%EA%B3%B1%EA%B7%BC_5" title="제곱근 5">제곱근 5</a> (<span class="nowrap">√<span style="border-top:1px solid; padding:0 0.1em;">5</span></span>)</li>
<li><a href="/wiki/%EB%B0%B1%EC%9D%80%EB%B9%84" class="mw-redirect" title="백은비">백은비</a> (<link rel="mw-deduplicated-inline-style" href="mw-data:TemplateStyles:r25030363"/><span class="texhtml">δ<sub><i>S</i></sub></span>)</li></ul>
<ul><li><a href="/wiki/E_(%EC%83%81%EC%88%98)" title="E (상수)">자연로그의 밑</a> (<link rel="mw-deduplicated-inline-style" href="mw-data:TemplateStyles:r25030363"/><span class="texhtml" style="font-style: italic;">e</span>)</li>
<li><a class="mw-selflink selflink">원주율</a> (<span style="font-family:'Times New Roman',serif;font-size:118%">π</span>)</li></ul>
</div></td><td class="navbox-image" rowspan="3" style="width:1px;padding:0px 0px 0px 2px"><div><a href="/wiki/%ED%8C%8C%EC%9D%BC:Gold,_square_root_of_2,_and_square_root_of_3_rectangles.png" class="image"><img alt="Gold, square root of 2, and square root of 3 rectangles.png" src="//upload.wikimedia.org/wikipedia/commons/thumb/3/34/Gold%2C_square_root_of_2%2C_and_square_root_of_3_rectangles.png/50px-Gold%2C_square_root_of_2%2C_and_square_root_of_3_rectangles.png" decoding="async" width="50" height="89" srcset="//upload.wikimedia.org/wikipedia/commons/thumb/3/34/Gold%2C_square_root_of_2%2C_and_square_root_of_3_rectangles.png/75px-Gold%2C_square_root_of_2%2C_and_square_root_of_3_rectangles.png 1.5x, //upload.wikimedia.org/wikipedia/commons/thumb/3/34/Gold%2C_square_root_of_2%2C_and_square_root_of_3_rectangles.png/100px-Gold%2C_square_root_of_2%2C_and_square_root_of_3_rectangles.png 2x" data-file-width="1047" data-file-height="1873" /></a></div></td></tr><tr><td colspan="2" class="navbox-list navbox-even hlist" style="width:100%;padding:0px"><div style="padding:0em 0.25em">
<ul><li>정신분열수</li>
<li><a href="/wiki/%EC%B4%88%EC%9B%94%EC%88%98" title="초월수">초월수</a></li>
<li>삼각법수</li></ul>
</div></td></tr><tr><td colspan="2" class="navbox-list navbox-odd hlist" style="width:100%;padding:0px"><div style="padding:0em 0.25em">
<ul><li><b>미해결</b>:</li>
<li><a href="/wiki/%EC%98%A4%EC%9D%BC%EB%9F%AC-%EB%A7%88%EC%8A%A4%EC%BC%80%EB%A1%9C%EB%8B%88_%EC%83%81%EC%88%98" title="오일러-마스케로니 상수">오일러-마스케로니</a> (<link rel="mw-deduplicated-inline-style" href="mw-data:TemplateStyles:r25030363"/><span class="texhtml" style="font-style: italic;">γ</span>)</li>
<li><a href="/wiki/%EC%B9%B4%ED%83%88%EB%9E%91_%EC%83%81%EC%88%98" title="카탈랑 상수">카탈랑 상수</a> (<link rel="mw-deduplicated-inline-style" href="mw-data:TemplateStyles:r25030363"/><span class="texhtml" style="font-style: italic;">C</span>)</li>
<li><a href="/wiki/2%ED%95%99%EB%85%84%EC%9D%98_%EA%BF%88" title="2학년의 꿈">2학년의 꿈</a></li>
<li><a href="/wiki/%ED%8C%8C%EC%9D%B4%EA%B2%90%EB%B0%94%EC%9B%80_%EC%83%81%EC%88%98" title="파이겐바움 상수">두 번째 파이겐바움</a> (<link rel="mw-deduplicated-inline-style" href="mw-data:TemplateStyles:r25030363"/><span class="texhtml" style="font-style: italic;">α</span>)</li>
<li><a href="/wiki/%ED%8C%8C%EC%9D%B4%EA%B2%90%EB%B0%94%EC%9B%80_%EC%83%81%EC%88%98" title="파이겐바움 상수">첫 번째 파이겐바움</a> (<link rel="mw-deduplicated-inline-style" href="mw-data:TemplateStyles:r25030363"/><span class="texhtml" style="font-style: italic;">δ</span>)</li></ul>
</div></td></tr></tbody></table></div>
<div role="navigation" class="navbox" aria-labelledby="수학_상수" style="padding:3px"><table class="nowraplinks hlist mw-collapsible autocollapse navbox-inner" style="border-spacing:0;background:transparent;color:inherit"><tbody><tr><th scope="col" class="navbox-title" colspan="2"><div class="plainlinks hlist navbar mini"><ul><li class="nv-view"><a href="/wiki/%ED%8B%80:%EC%88%98%ED%95%99_%EC%83%81%EC%88%98" title="틀:수학 상수"><abbr title="이 틀을 보기" style=";;background:none transparent;border:none;-moz-box-shadow:none;-webkit-box-shadow:none;box-shadow:none; padding:0;">v</abbr></a></li><li class="nv-talk"><a href="/w/index.php?title=%ED%8B%80%ED%86%A0%EB%A1%A0:%EC%88%98%ED%95%99_%EC%83%81%EC%88%98&action=edit&redlink=1" class="new" title="틀토론:수학 상수 (없는 문서)"><abbr title="이 틀에 대한 토론" style=";;background:none transparent;border:none;-moz-box-shadow:none;-webkit-box-shadow:none;box-shadow:none; padding:0;">t</abbr></a></li><li class="nv-edit"><a class="external text" href="https://ko.wikipedia.org/w/index.php?title=%ED%8B%80:%EC%88%98%ED%95%99_%EC%83%81%EC%88%98&action=edit"><abbr title="이 틀을 편집하기" style=";;background:none transparent;border:none;-moz-box-shadow:none;-webkit-box-shadow:none;box-shadow:none; padding:0;">e</abbr></a></li></ul></div><div id="수학_상수" style="font-size:114%;margin:0 4em"><a href="/wiki/%EC%88%98%ED%95%99_%EC%83%81%EC%88%98" title="수학 상수">수학 상수</a></div></th></tr><tr><th scope="row" class="navbox-group" style="width:1%"><a href="/wiki/%EC%A0%95%EC%88%98" title="정수">정수</a></th><td class="navbox-list navbox-odd" style="text-align:left;border-left-width:2px;border-left-style:solid;width:100%;padding:0px"><div style="padding:0em 0.25em">
<ul><li><a href="/wiki/-1" class="mw-redirect" title="-1">-1</a></li>
<li><a href="/wiki/0" title="0">0</a></li>
<li><a href="/wiki/1" title="1">1</a></li>
<li><a href="/wiki/2" title="2">2</a></li>
<li><a href="/wiki/3" title="3">3</a></li></ul>
</div></td></tr><tr><th scope="row" class="navbox-group" style="width:1%"><a href="/wiki/%ED%97%88%EC%88%98" title="허수">허수</a></th><td class="navbox-list navbox-even" style="text-align:left;border-left-width:2px;border-left-style:solid;width:100%;padding:0px"><div style="padding:0em 0.25em">
<ul><li><a href="/wiki/%ED%97%88%EC%88%98_%EB%8B%A8%EC%9C%84" title="허수 단위">i</a> (<span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle i}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>i</mi>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle i}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/add78d8608ad86e54951b8c8bd6c8d8416533d20" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.338ex; width:0.802ex; height:2.176ex;" alt="i"/></span>)</li></ul>
</div></td></tr><tr><th scope="row" class="navbox-group" style="width:1%"><a href="/wiki/%EC%B4%88%EC%9B%94%EC%88%98" title="초월수">초월수</a></th><td class="navbox-list navbox-odd" style="text-align:left;border-left-width:2px;border-left-style:solid;width:100%;padding:0px"><div style="padding:0em 0.25em">
<ul><li><a class="mw-selflink selflink">π</a></li>
<li><a href="/wiki/E_(%EC%83%81%EC%88%98)" title="E (상수)">e</a> (<span class="mwe-math-element"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle e}">
<semantics>
<mrow class="MJX-TeXAtom-ORD">
<mstyle displaystyle="true" scriptlevel="0">
<mi>e</mi>
</mstyle>
</mrow>
<annotation encoding="application/x-tex">{\displaystyle e}</annotation>
</semantics>
</math></span><img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/cd253103f0876afc68ebead27a5aa9867d927467" class="mwe-math-fallback-image-inline" aria-hidden="true" style="vertical-align: -0.338ex; width:1.083ex; height:1.676ex;" alt="e"/></span>)</li></ul>
</div></td></tr><tr><th scope="row" class="navbox-group" style="width:1%"><a href="/wiki/%EB%AC%B4%EB%A6%AC%EC%88%98" title="무리수">무리수</a></th><td class="navbox-list navbox-even" style="text-align:left;border-left-width:2px;border-left-style:solid;width:100%;padding:0px"><div style="padding:0em 0.25em">
<ul><li><a href="/wiki/%EC%95%84%ED%8E%98%EB%A6%AC_%EC%83%81%EC%88%98" title="아페리 상수">아페리 상수</a></li>
<li><a href="/wiki/%EC%97%90%EB%A5%B4%EB%90%98%EC%8B%9C-%EB%B3%B4%EC%96%B4%EC%99%80%EC%9D%B8_%EC%83%81%EC%88%98" title="에르되시-보어와인 상수">에르되시-보어와인 상수</a></li>
<li><a href="/wiki/%EC%A0%9C%EA%B3%B1%EA%B7%BC_2" title="제곱근 2">√2</a></li>
<li><a href="/wiki/%ED%99%A9%EA%B8%88%EB%B9%84" title="황금비">φ</a></li></ul>
</div></td></tr><tr><th scope="row" class="navbox-group" style="width:1%">기타</th><td class="navbox-list navbox-odd" style="text-align:left;border-left-width:2px;border-left-style:solid;width:100%;padding:0px"><div style="padding:0em 0.25em">
<ul><li><a href="/wiki/%EB%93%9C_%EB%B8%8C%EB%A3%A8%EC%9D%B8-%EB%89%B4%EB%A8%BC_%EC%83%81%EC%88%98" title="드 브루인-뉴먼 상수">드 브루인-뉴먼 상수</a></li>
<li><a href="/wiki/%EB%9D%BC%EB%A7%88%EB%88%84%EC%9E%94-%EC%86%94%EB%93%9C%EB%84%88_%EC%83%81%EC%88%98" title="라마누잔-솔드너 상수">라마누잔-솔드너 상수</a></li>
<li><a href="/wiki/%EB%A5%B4%EC%9E%A5%EB%93%9C%EB%A5%B4_%EC%83%81%EC%88%98" title="르장드르 상수">르장드르 상수</a></li>
<li><a href="/wiki/%EB%A7%88%EC%9D%B4%EC%85%80-%EB%A9%94%EB%A5%B4%ED%85%90%EC%8A%A4_%EC%83%81%EC%88%98" title="마이셀-메르텐스 상수">마이셀-메르텐스 상수</a></li>
<li><a href="/wiki/%EB%B9%84%EC%8A%88%EB%B0%94%EB%82%98%ED%8A%B8_%EC%83%81%EC%88%98" title="비슈바나트 상수">비슈바나트 상수</a></li>
<li><a href="/wiki/%EB%B8%8C%EB%A3%AC_%EC%83%81%EC%88%98" title="브룬 상수">브룬 상수</a></li>
<li><a href="/wiki/%EC%8C%8D%EB%91%A5%EC%9D%B4_%EC%86%8C%EC%88%98_%EC%83%81%EC%88%98" title="쌍둥이 소수 상수">쌍둥이 소수 상수</a></li>
<li><a href="/wiki/%EC%98%A4%EC%9D%BC%EB%9F%AC-%EB%A7%88%EC%8A%A4%EC%BC%80%EB%A1%9C%EB%8B%88_%EC%83%81%EC%88%98" title="오일러-마스케로니 상수">오일러-마스케로니 상수</a></li>
<li><a href="/wiki/%EC%97%A0%EB%B8%8C%EB%A6%AC-%ED%8A%B8%EB%A0%88%ED%8E%98%ED%85%90_%EC%83%81%EC%88%98" title="엠브리-트레페텐 상수">엠브리-트레페텐 상수</a></li>
<li><a href="/wiki/%EC%B9%B4%ED%83%88%EB%9E%91_%EC%83%81%EC%88%98" title="카탈랑 상수">카탈랑 상수</a></li>
<li><a href="/wiki/%ED%8C%8C%EC%9D%B4%EA%B2%90%EB%B0%94%EC%9B%80_%EC%83%81%EC%88%98" title="파이겐바움 상수">파이겐바움 상수</a></li></ul>
</div></td></tr></tbody></table></div>
<div role="navigation" class="navbox authority-control" aria-labelledby="전거_통제_frameless_&#124;text-top_&#124;10px_&#124;alt=위키데이터에서_편집하기_&#124;link=https&#58;//www.wikidata.org/wiki/Q167&#124;위키데이터에서_편집하기" style="padding:3px"><table class="nowraplinks hlist navbox-inner" style="border-spacing:0;background:transparent;color:inherit"><tbody><tr><th id="전거_통제_frameless_&#124;text-top_&#124;10px_&#124;alt=위키데이터에서_편집하기_&#124;link=https&#58;//www.wikidata.org/wiki/Q167&#124;위키데이터에서_편집하기" scope="row" class="navbox-group" style="width:1%"><a href="/wiki/%EC%9C%84%ED%82%A4%EB%B0%B1%EA%B3%BC:%EC%A0%84%EA%B1%B0_%ED%86%B5%EC%A0%9C" title="위키백과:전거 통제">전거 통제</a> <a href="https://www.wikidata.org/wiki/Q167" title="위키데이터에서 편집하기"><img alt="위키데이터에서 편집하기" src="//upload.wikimedia.org/wikipedia/commons/thumb/8/8a/OOjs_UI_icon_edit-ltr-progressive.svg/10px-OOjs_UI_icon_edit-ltr-progressive.svg.png" decoding="async" width="10" height="10" style="vertical-align: text-top" srcset="//upload.wikimedia.org/wikipedia/commons/thumb/8/8a/OOjs_UI_icon_edit-ltr-progressive.svg/15px-OOjs_UI_icon_edit-ltr-progressive.svg.png 1.5x, //upload.wikimedia.org/wikipedia/commons/thumb/8/8a/OOjs_UI_icon_edit-ltr-progressive.svg/20px-OOjs_UI_icon_edit-ltr-progressive.svg.png 2x" data-file-width="20" data-file-height="20" /></a></th><td class="navbox-list navbox-odd" style="text-align:left;border-left-width:2px;border-left-style:solid;width:100%;padding:0px"><div style="padding:0em 0.25em">
<ul><li><span class="nowrap"><a href="/wiki/%EA%B2%8C%EB%A7%88%EC%9D%B8%EC%9E%90%EB%A9%94_%EB%85%B8%EB%A6%84%EB%8B%A4%ED%83%80%EC%9D%B4" title="게마인자메 노름다타이">GND</a>: <span class="uid"><a rel="nofollow" class="external text" href="https://d-nb.info/gnd/4174646-6">4174646-6</a></span></span></li>
<li><span class="nowrap"><a href="/wiki/%EB%AF%B8%EA%B5%AD_%EC%9D%98%ED%9A%8C%EB%8F%84%EC%84%9C%EA%B4%80_%EC%A0%9C%EC%96%B4_%EB%B2%88%ED%98%B8" title="미국 의회도서관 제어 번호">LCCN</a>: <span class="uid"><a rel="nofollow" class="external text" href="https://id.loc.gov/authorities/subjects/sh85101712">sh85101712</a></span></span></li>
<li><span class="nowrap"><a href="/wiki/%EC%9D%BC%EB%B3%B8_%EA%B5%AD%EB%A6%BD%EA%B5%AD%ED%9A%8C%EB%8F%84%EC%84%9C%EA%B4%80" title="일본 국립국회도서관">NDL</a>: <span class="uid"><a rel="nofollow" class="external text" href="https://id.ndl.go.jp/auth/ndlna/00562015">00562015</a></span></span></li></ul>
</div></td></tr></tbody></table></div>
<!--
NewPP limit report
Parsed by mw1373
Cached time: 20200714210535
Cache expiry: 2592000
Dynamic content: false
Complications: [vary‐revision‐sha1]
CPU time usage: 0.720 seconds
Real time usage: 1.038 seconds
Preprocessor visited node count: 5673/1000000
Post‐expand include size: 73730/2097152 bytes
Template argument size: 4580/2097152 bytes
Highest expansion depth: 15/40
Expensive parser function count: 3/500
Unstrip recursion depth: 1/20
Unstrip post‐expand size: 70361/5000000 bytes
Lua time usage: 0.164/10.000 seconds
Lua memory usage: 4.96 MB/50 MB
Number of Wikibase entities loaded: 1/400
-->
<!--
Transclusion expansion time report (%,ms,calls,template)
100.00% 680.733 1 -total
39.85% 271.282 1 틀:각주
20.92% 142.415 17 틀:ISBN
14.06% 95.703 1 틀:무리수
13.43% 91.438 2 틀:둘러보기_상자
11.64% 79.207 4 틀:서적_인용
10.67% 72.637 17 틀:Catalog_lookup_link
9.56% 65.064 1 틀:좋은_글
9.02% 61.395 1 틀:상단_아이콘
7.10% 48.316 1 틀:Category_handler
-->
<!-- Saved in parser cache with key kowiki:pcache:idhash:284-0!canonical!math=5 and timestamp 20200714210534 and revision id 27000186
-->
</div><noscript><img src="//ko.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1x1" alt="" title="" width="1" height="1" style="border: none; position: absolute;" /></noscript></div>
<div class="printfooter">원본 주소 "<a dir="ltr" href="https://ko.wikipedia.org/w/index.php?title=원주율&oldid=27000186">https://ko.wikipedia.org/w/index.php?title=원주율&oldid=27000186</a>"</div>
<div id="catlinks" class="catlinks" data-mw="interface"><div id="mw-normal-catlinks" class="mw-normal-catlinks"><a href="/wiki/%ED%8A%B9%EC%88%98:%EB%B6%84%EB%A5%98" title="특수:분류">분류</a>: <ul><li><a href="/wiki/%EB%B6%84%EB%A5%98:%EC%9B%90%EC%A3%BC%EC%9C%A8" title="분류:원주율">원주율</a></li><li><a href="/wiki/%EB%B6%84%EB%A5%98:%EB%B9%84_(%EC%88%98%ED%95%99)" title="분류:비 (수학)">비 (수학)</a></li><li><a href="/wiki/%EB%B6%84%EB%A5%98:%EC%88%98%ED%95%99_%EC%83%81%EC%88%98" title="분류:수학 상수">수학 상수</a></li><li><a href="/wiki/%EB%B6%84%EB%A5%98:%EC%B4%88%EC%9B%94%EC%88%98" title="분류:초월수">초월수</a></li><li><a href="/wiki/%EB%B6%84%EB%A5%98:%EB%AC%B4%EB%A6%AC%EC%88%98" title="분류:무리수">무리수</a></li><li><a href="/wiki/%EB%B6%84%EB%A5%98:%EB%B3%B5%EC%86%8C%ED%95%B4%EC%84%9D%ED%95%99" title="분류:복소해석학">복소해석학</a></li></ul></div><div id="mw-hidden-catlinks" class="mw-hidden-catlinks mw-hidden-cats-hidden">숨은 분류: <ul><li><a href="/wiki/%EB%B6%84%EB%A5%98:CS1_%EA%B4%80%EB%A6%AC_-_%EC%B6%94%EA%B0%80_%EB%AC%B8%EA%B5%AC" title="분류:CS1 관리 - 추가 문구">CS1 관리 - 추가 문구</a></li><li><a href="/wiki/%EB%B6%84%EB%A5%98:CS1_-_%EC%98%81%EC%96%B4_%EC%9D%B8%EC%9A%A9_(en)" title="분류:CS1 - 영어 인용 (en)">CS1 - 영어 인용 (en)</a></li><li><a href="/wiki/%EB%B6%84%EB%A5%98:%EA%B9%A8%EC%A7%84_%EB%A7%81%ED%81%AC%EB%A5%BC_%EA%B0%80%EC%A7%80%EA%B3%A0_%EC%9E%88%EB%8A%94_%EB%AC%B8%EC%84%9C" title="분류:깨진 링크를 가지고 있는 문서">깨진 링크를 가지고 있는 문서</a></li><li><a href="/wiki/%EB%B6%84%EB%A5%98:%EC%A2%8B%EC%9D%80_%EA%B8%80" title="분류:좋은 글">좋은 글</a></li><li><a href="/wiki/%EB%B6%84%EB%A5%98:%EB%AC%B8%ED%99%94%EC%96%B4_%ED%91%9C%EA%B8%B0%EB%A5%BC_%ED%8F%AC%ED%95%A8%ED%95%9C_%EB%AC%B8%EC%84%9C" title="분류:문화어 표기를 포함한 문서">문화어 표기를 포함한 문서</a></li><li><a href="/wiki/%EB%B6%84%EB%A5%98:GND_%EC%8B%9D%EB%B3%84%EC%9E%90%EB%A5%BC_%ED%8F%AC%ED%95%A8%ED%95%9C_%EC%9C%84%ED%82%A4%EB%B0%B1%EA%B3%BC_%EB%AC%B8%EC%84%9C" title="분류:GND 식별자를 포함한 위키백과 문서">GND 식별자를 포함한 위키백과 문서</a></li><li><a href="/wiki/%EB%B6%84%EB%A5%98:LCCN_%EC%8B%9D%EB%B3%84%EC%9E%90%EB%A5%BC_%ED%8F%AC%ED%95%A8%ED%95%9C_%EC%9C%84%ED%82%A4%EB%B0%B1%EA%B3%BC_%EB%AC%B8%EC%84%9C" title="분류:LCCN 식별자를 포함한 위키백과 문서">LCCN 식별자를 포함한 위키백과 문서</a></li><li><a href="/wiki/%EB%B6%84%EB%A5%98:NDL_%EC%8B%9D%EB%B3%84%EC%9E%90%EB%A5%BC_%ED%8F%AC%ED%95%A8%ED%95%9C_%EC%9C%84%ED%82%A4%EB%B0%B1%EA%B3%BC_%EB%AC%B8%EC%84%9C" title="분류:NDL 식별자를 포함한 위키백과 문서">NDL 식별자를 포함한 위키백과 문서</a></li></ul></div></div>
</div>
</div>
<div id='mw-data-after-content'>
<div class="read-more-container"></div>
</div>
<div id="mw-navigation">
<h2>둘러보기 메뉴</h2>
<div id="mw-head">
<!-- Please do not use role attribute as CSS selector, it is deprecated. -->
<nav id="p-personal" class="vector-menu" aria-labelledby="p-personal-label" role="navigation"
>
<h3 id="p-personal-label">
<span>개인 도구</span>
</h3>
<!-- Please do not use the .body class, it is deprecated. -->
<div class="body vector-menu-content">
<!-- Please do not use the .menu class, it is deprecated. -->
<ul class="vector-menu-content-list"><li id="pt-anonuserpage">로그인하지 않음</li><li id="pt-anontalk"><a href="/wiki/%ED%8A%B9%EC%88%98:%EB%82%B4%EC%82%AC%EC%9A%A9%EC%9E%90%ED%86%A0%EB%A1%A0" title="현재 사용하는 IP 주소에 대한 토론 문서 [n]" accesskey="n">토론</a></li><li id="pt-anoncontribs"><a href="/wiki/%ED%8A%B9%EC%88%98:%EB%82%B4%EA%B8%B0%EC%97%AC" title="이 IP 주소의 편집 목록 [y]" accesskey="y">기여</a></li><li id="pt-createaccount"><a href="/w/index.php?title=%ED%8A%B9%EC%88%98:%EA%B3%84%EC%A0%95%EB%A7%8C%EB%93%A4%EA%B8%B0&returnto=%EC%9B%90%EC%A3%BC%EC%9C%A8" title="계정을 만들고 로그인하는 것이 좋습니다; 하지만, 필수는 아닙니다">계정 만들기</a></li><li id="pt-login"><a href="/w/index.php?title=%ED%8A%B9%EC%88%98:%EB%A1%9C%EA%B7%B8%EC%9D%B8&returnto=%EC%9B%90%EC%A3%BC%EC%9C%A8" title="위키백과에 로그인하면 여러가지 편리한 기능을 사용할 수 있습니다. [o]" accesskey="o">로그인</a></li></ul>
</div>
</nav>
<div id="left-navigation">
<!-- Please do not use role attribute as CSS selector, it is deprecated. -->
<nav id="p-namespaces" class="vector-menu vector-menu-tabs vectorTabs" aria-labelledby="p-namespaces-label" role="navigation"
>
<h3 id="p-namespaces-label">
<span>이름공간</span>
</h3>
<!-- Please do not use the .body class, it is deprecated. -->
<div class="body vector-menu-content">
<!-- Please do not use the .menu class, it is deprecated. -->
<ul class="vector-menu-content-list"><li id="ca-nstab-main" class="selected"><a href="/wiki/%EC%9B%90%EC%A3%BC%EC%9C%A8" title="본문 보기 [c]" accesskey="c">문서</a></li><li id="ca-talk"><a href="/wiki/%ED%86%A0%EB%A1%A0:%EC%9B%90%EC%A3%BC%EC%9C%A8" rel="discussion" title="문서의 내용에 대한 토론 문서 [t]" accesskey="t">토론</a></li></ul>
</div>
</nav>
<!-- Please do not use role attribute as CSS selector, it is deprecated. -->
<nav id="p-variants" class="vector-menu-empty emptyPortlet vector-menu vector-menu-dropdown vectorMenu" aria-labelledby="p-variants-label" role="navigation"
>
<input type="checkbox" class="vector-menu-checkbox vectorMenuCheckbox" aria-labelledby="p-variants-label" />
<h3 id="p-variants-label">
<span>변수</span>
</h3>
<!-- Please do not use the .body class, it is deprecated. -->
<div class="body vector-menu-content">
<!-- Please do not use the .menu class, it is deprecated. -->
<ul class="menu vector-menu-content-list"></ul>
</div>
</nav>
</div>
<div id="right-navigation">
<!-- Please do not use role attribute as CSS selector, it is deprecated. -->
<nav id="p-views" class="vector-menu vector-menu-tabs vectorTabs" aria-labelledby="p-views-label" role="navigation"
>
<h3 id="p-views-label">
<span>보기</span>
</h3>
<!-- Please do not use the .body class, it is deprecated. -->
<div class="body vector-menu-content">
<!-- Please do not use the .menu class, it is deprecated. -->
<ul class="vector-menu-content-list"><li id="ca-view" class="collapsible selected"><a href="/wiki/%EC%9B%90%EC%A3%BC%EC%9C%A8">읽기</a></li><li id="ca-edit" class="collapsible"><a href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8&action=edit" title="이 문서 편집하기 [e]" accesskey="e">편집</a></li><li id="ca-history" class="collapsible"><a href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8&action=history" title="이 문서의 과거 편집 내역입니다. [h]" accesskey="h">역사 보기</a></li></ul>
</div>
</nav>
<!-- Please do not use role attribute as CSS selector, it is deprecated. -->
<nav id="p-cactions" class="vector-menu-empty emptyPortlet vector-menu vector-menu-dropdown vectorMenu" aria-labelledby="p-cactions-label" role="navigation"
>
<input type="checkbox" class="vector-menu-checkbox vectorMenuCheckbox" aria-labelledby="p-cactions-label" />
<h3 id="p-cactions-label">
<span>더 보기</span>
</h3>
<!-- Please do not use the .body class, it is deprecated. -->
<div class="body vector-menu-content">
<!-- Please do not use the .menu class, it is deprecated. -->
<ul class="menu vector-menu-content-list"></ul>
</div>
</nav>
<div id="p-search" role="search">
<h3 >
<label for="searchInput">검색</label>
</h3>
<form action="/w/index.php" id="searchform">
<div id="simpleSearch">
<input type="search" name="search" placeholder="위키백과 검색" title="위키백과 검색 [f]" accesskey="f" id="searchInput"/>
<input type="hidden" name="title" value="특수:검색">
<input type="submit" name="fulltext" value="검색" title="이 문자열이 포함된 문서 검색" id="mw-searchButton" class="searchButton mw-fallbackSearchButton"/>
<input type="submit" name="go" value="보기" title="이 이름의 문서가 존재하면 그 문서로 바로 가기" id="searchButton" class="searchButton"/>
</div>
</form>
</div>
</div>
</div>
<div id="mw-panel">
<div id="p-logo" role="banner">
<a title="대문으로 가기" class="mw-wiki-logo" href="/wiki/%EC%9C%84%ED%82%A4%EB%B0%B1%EA%B3%BC:%EB%8C%80%EB%AC%B8"></a>
</div>
<!-- Please do not use role attribute as CSS selector, it is deprecated. -->
<nav id="p-navigation" class="vector-menu vector-menu-portal portal portal-first" aria-labelledby="p-navigation-label" role="navigation"
>
<h3 id="p-navigation-label">
<span>둘러보기</span>
</h3>
<!-- Please do not use the .body class, it is deprecated. -->
<div class="body vector-menu-content">
<!-- Please do not use the .menu class, it is deprecated. -->
<ul class="vector-menu-content-list"><li id="n-mainpage-description"><a href="/wiki/%EC%9C%84%ED%82%A4%EB%B0%B1%EA%B3%BC:%EB%8C%80%EB%AC%B8" title="대문으로 가기 [z]" accesskey="z">대문</a></li><li id="n-recentchanges"><a href="/wiki/%ED%8A%B9%EC%88%98:%EC%B5%9C%EA%B7%BC%EB%B0%94%EB%80%9C" title="위키의 최근 바뀐 목록 [r]" accesskey="r">최근 바뀜</a></li><li id="n-currentevents"><a href="/wiki/%ED%8F%AC%ED%84%B8:%EC%9A%94%EC%A6%98_%ED%99%94%EC%A0%9C" title="최근의 소식 알아 보기">요즘 화제</a></li><li id="n-randompage"><a href="/wiki/%ED%8A%B9%EC%88%98:%EC%9E%84%EC%9D%98%EB%AC%B8%EC%84%9C" title="무작위로 선택된 문서 불러오기 [x]" accesskey="x">임의의 문서로</a></li><li id="n-sitesupport"><a href="//donate.wikimedia.org/wiki/Special:FundraiserRedirector?utm_source=donate&utm_medium=sidebar&utm_campaign=C13_ko.wikipedia.org&uselang=ko" title="지원을 기다립니다">기부</a></li></ul>
</div>
</nav>
<!-- Please do not use role attribute as CSS selector, it is deprecated. -->
<nav id="p-사용자 모임" class="vector-menu vector-menu-portal portal" aria-labelledby="p-사용자 모임-label" role="navigation"
>
<h3 id="p-사용자 모임-label">
<span>사용자 모임</span>
</h3>
<!-- Please do not use the .body class, it is deprecated. -->
<div class="body vector-menu-content">
<!-- Please do not use the .menu class, it is deprecated. -->
<ul class="vector-menu-content-list"><li id="n-projectchat"><a href="/wiki/%EC%9C%84%ED%82%A4%EB%B0%B1%EA%B3%BC:%EC%82%AC%EB%9E%91%EB%B0%A9">사랑방</a></li><li id="n-portal"><a href="/wiki/%EC%9C%84%ED%82%A4%EB%B0%B1%EA%B3%BC:%EC%82%AC%EC%9A%A9%EC%9E%90_%EB%AA%A8%EC%9E%84" title="위키백과 참여자를 위한 토론/대화 공간입니다.">사용자 모임</a></li><li id="n-request"><a href="/wiki/%EC%9C%84%ED%82%A4%EB%B0%B1%EA%B3%BC:%EC%9A%94%EC%B2%AD">관리 요청</a></li><li id="n-studentcamp"><a href="/wiki/%EC%9C%84%ED%82%A4%EB%B0%B1%EA%B3%BC:%ED%95%99%EC%83%9D_%EC%BA%A0%ED%94%84">학생 캠프</a></li></ul>
</div>
</nav>
<!-- Please do not use role attribute as CSS selector, it is deprecated. -->
<nav id="p-편집 안내" class="vector-menu vector-menu-portal portal" aria-labelledby="p-편집 안내-label" role="navigation"
>
<h3 id="p-편집 안내-label">
<span>편집 안내</span>
</h3>
<!-- Please do not use the .body class, it is deprecated. -->
<div class="body vector-menu-content">
<!-- Please do not use the .menu class, it is deprecated. -->
<ul class="vector-menu-content-list"><li id="n-help"><a href="/wiki/%EC%9C%84%ED%82%A4%EB%B0%B1%EA%B3%BC:%EB%8F%84%EC%9B%80%EB%A7%90" title="도움말">도움말</a></li><li id="n-policy"><a href="/wiki/%EC%9C%84%ED%82%A4%EB%B0%B1%EA%B3%BC:%EC%A0%95%EC%B1%85%EA%B3%BC_%EC%A7%80%EC%B9%A8">정책과 지침</a></li><li id="n-qna"><a href="/wiki/%EC%9C%84%ED%82%A4%EB%B0%B1%EA%B3%BC:%EC%A7%88%EB%AC%B8%EB%B0%A9">질문방</a></li></ul>
</div>
</nav>
<!-- Please do not use role attribute as CSS selector, it is deprecated. -->
<nav id="p-tb" class="vector-menu vector-menu-portal portal" aria-labelledby="p-tb-label" role="navigation"
>
<h3 id="p-tb-label">
<span>도구</span>
</h3>
<!-- Please do not use the .body class, it is deprecated. -->
<div class="body vector-menu-content">
<!-- Please do not use the .menu class, it is deprecated. -->
<ul class="vector-menu-content-list"><li id="t-whatlinkshere"><a href="/wiki/%ED%8A%B9%EC%88%98:%EA%B0%80%EB%A6%AC%ED%82%A4%EB%8A%94%EB%AC%B8%EC%84%9C/%EC%9B%90%EC%A3%BC%EC%9C%A8" title="여기를 가리키는 모든 위키 문서의 목록 [j]" accesskey="j">여기를 가리키는 문서</a></li><li id="t-recentchangeslinked"><a href="/wiki/%ED%8A%B9%EC%88%98:%EB%A7%81%ED%81%AC%EC%B5%9C%EA%B7%BC%EB%B0%94%EB%80%9C/%EC%9B%90%EC%A3%BC%EC%9C%A8" rel="nofollow" title="이 문서에서 링크한 문서의 최근 바뀜 [k]" accesskey="k">가리키는 글의 최근 바뀜</a></li><li id="t-upload"><a href="/wiki/위키백과:파일_올리기" title="파일 올리기 [u]" accesskey="u">파일 올리기</a></li><li id="t-specialpages"><a href="/wiki/%ED%8A%B9%EC%88%98:%ED%8A%B9%EC%88%98%EB%AC%B8%EC%84%9C" title="모든 특수 문서의 목록 [q]" accesskey="q">특수 문서 목록</a></li><li id="t-permalink"><a href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8&oldid=27000186" title="문서의 이 판에 대한 고유링크">고유 링크</a></li><li id="t-info"><a href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8&action=info" title="이 문서에 대한 자세한 정보">문서 정보</a></li><li id="t-cite"><a href="/w/index.php?title=%ED%8A%B9%EC%88%98:%EC%9D%B4%EB%AC%B8%EC%84%9C%EC%9D%B8%EC%9A%A9&page=%EC%9B%90%EC%A3%BC%EC%9C%A8&id=27000186&wpFormIdentifier=titleform" title="이 문서를 인용하는 방법에 대한 정보">이 문서 인용하기</a></li><li id="t-wikibase"><a href="https://www.wikidata.org/wiki/Special:EntityPage/Q167" title="데이터 저장소에 연결된 항목을 가리키는 링크 [g]" accesskey="g">위키데이터 항목</a></li></ul>
</div>
</nav>
<!-- Please do not use role attribute as CSS selector, it is deprecated. -->
<nav id="p-coll-print_export" class="vector-menu vector-menu-portal portal" aria-labelledby="p-coll-print_export-label" role="navigation"
>
<h3 id="p-coll-print_export-label">
<span>인쇄/내보내기</span>
</h3>
<!-- Please do not use the .body class, it is deprecated. -->
<div class="body vector-menu-content">
<!-- Please do not use the .menu class, it is deprecated. -->
<ul class="vector-menu-content-list"><li id="coll-create_a_book"><a href="/w/index.php?title=%ED%8A%B9%EC%88%98:%EC%B1%85&bookcmd=book_creator&referer=%EC%9B%90%EC%A3%BC%EC%9C%A8">책 만들기</a></li><li id="coll-download-as-rl"><a href="/w/index.php?title=%ED%8A%B9%EC%88%98:ElectronPdf&page=%EC%9B%90%EC%A3%BC%EC%9C%A8&action=show-download-screen">PDF로 다운로드</a></li><li id="t-print"><a href="/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8&printable=yes" title="이 문서의 인쇄용 판 [p]" accesskey="p">인쇄용 판</a></li></ul>
</div>
</nav>
<!-- Please do not use role attribute as CSS selector, it is deprecated. -->
<nav id="p-wikibase-otherprojects" class="vector-menu vector-menu-portal portal" aria-labelledby="p-wikibase-otherprojects-label" role="navigation"
>
<h3 id="p-wikibase-otherprojects-label">
<span>다른 프로젝트</span>
</h3>
<!-- Please do not use the .body class, it is deprecated. -->
<div class="body vector-menu-content">
<!-- Please do not use the .menu class, it is deprecated. -->
<ul class="vector-menu-content-list"><li class="wb-otherproject-link wb-otherproject-commons"><a href="https://commons.wikimedia.org/wiki/Category:Pi" hreflang="en">위키미디어 공용</a></li></ul>
</div>
</nav>
<!-- Please do not use role attribute as CSS selector, it is deprecated. -->
<nav id="p-lang" class="vector-menu vector-menu-portal portal" aria-labelledby="p-lang-label" role="navigation"
>
<h3 id="p-lang-label">
<span>다른 언어</span>
</h3>
<!-- Please do not use the .body class, it is deprecated. -->
<div class="body vector-menu-content">
<!-- Please do not use the .menu class, it is deprecated. -->
<ul class="vector-menu-content-list"><li class="interlanguage-link interwiki-pt"><a href="https://pt.wikipedia.org/wiki/Pi" title="Pi – 포르투갈어" lang="pt" hreflang="pt" class="interlanguage-link-target">Português</a></li><li class="interlanguage-link interwiki-it"><a href="https://it.wikipedia.org/wiki/Pi_greco" title="Pi greco – 이탈리아어" lang="it" hreflang="it" class="interlanguage-link-target">Italiano</a></li><li class="interlanguage-link interwiki-fr"><a href="https://fr.wikipedia.org/wiki/Pi" title="Pi – 프랑스어" lang="fr" hreflang="fr" class="interlanguage-link-target">Français</a></li><li class="interlanguage-link interwiki-als"><a href="https://als.wikipedia.org/wiki/Pi_(Mathematik)" title="Pi (Mathematik) – Alemannisch" lang="gsw" hreflang="gsw" class="interlanguage-link-target">Alemannisch</a></li><li class="interlanguage-link interwiki-am"><a href="https://am.wikipedia.org/wiki/%E1%8D%93%E1%8B%AD" title="ፓይ – 암하라어" lang="am" hreflang="am" class="interlanguage-link-target">አማርኛ</a></li><li class="interlanguage-link interwiki-an"><a href="https://an.wikipedia.org/wiki/Numero_%CF%80" title="Numero π – 아라곤어" lang="an" hreflang="an" class="interlanguage-link-target">Aragonés</a></li><li class="interlanguage-link interwiki-as"><a href="https://as.wikipedia.org/wiki/%E0%A6%AA%E0%A6%BE%E0%A6%87" title="পাই – 아삼어" lang="as" hreflang="as" class="interlanguage-link-target">অসমীয়া</a></li><li class="interlanguage-link interwiki-az"><a href="https://az.wikipedia.org/wiki/Pi_(%C9%99d%C9%99d)" title="Pi (ədəd) – 아제르바이잔어" lang="az" hreflang="az" class="interlanguage-link-target">Azərbaycanca</a></li><li class="interlanguage-link interwiki-be"><a href="https://be.wikipedia.org/wiki/%D0%9F%D1%96" title="Пі – 벨라루스어" lang="be" hreflang="be" class="interlanguage-link-target">Беларуская</a></li><li class="interlanguage-link interwiki-bg"><a href="https://bg.wikipedia.org/wiki/%D0%9F%D0%B8" title="Пи – 불가리아어" lang="bg" hreflang="bg" class="interlanguage-link-target">Български</a></li><li class="interlanguage-link interwiki-bjn"><a href="https://bjn.wikipedia.org/wiki/Pi" title="Pi – Banjar" lang="bjn" hreflang="bjn" class="interlanguage-link-target">Banjar</a></li><li class="interlanguage-link interwiki-bn"><a href="https://bn.wikipedia.org/wiki/%E0%A6%AA%E0%A6%BE%E0%A6%87" title="পাই – 벵골어" lang="bn" hreflang="bn" class="interlanguage-link-target">বাংলা</a></li><li class="interlanguage-link interwiki-bs"><a href="https://bs.wikipedia.org/wiki/Pi" title="Pi – 보스니아어" lang="bs" hreflang="bs" class="interlanguage-link-target">Bosanski</a></li><li class="interlanguage-link interwiki-ceb"><a href="https://ceb.wikipedia.org/wiki/Pi" title="Pi – 세부아노어" lang="ceb" hreflang="ceb" class="interlanguage-link-target">Cebuano</a></li><li class="interlanguage-link interwiki-da"><a href="https://da.wikipedia.org/wiki/Pi_(tal)" title="Pi (tal) – 덴마크어" lang="da" hreflang="da" class="interlanguage-link-target">Dansk</a></li><li class="interlanguage-link interwiki-dsb"><a href="https://dsb.wikipedia.org/wiki/Konstanta_%CF%80" title="Konstanta π – 저지 소르비아어" lang="dsb" hreflang="dsb" class="interlanguage-link-target">Dolnoserbski</a></li><li class="interlanguage-link interwiki-et"><a href="https://et.wikipedia.org/wiki/Pii" title="Pii – 에스토니아어" lang="et" hreflang="et" class="interlanguage-link-target">Eesti</a></li><li class="interlanguage-link interwiki-eu"><a href="https://eu.wikipedia.org/wiki/Pi_(zenbakia)" title="Pi (zenbakia) – 바스크어" lang="eu" hreflang="eu" class="interlanguage-link-target">Euskara</a></li><li class="interlanguage-link interwiki-ext"><a href="https://ext.wikipedia.org/wiki/N%C3%BAmiru_%CF%80" title="Númiru π – Extremaduran" lang="ext" hreflang="ext" class="interlanguage-link-target">Estremeñu</a></li><li class="interlanguage-link interwiki-fa"><a href="https://fa.wikipedia.org/wiki/%D8%B9%D8%AF%D8%AF_%D9%BE%DB%8C" title="عدد پی – 페르시아어" lang="fa" hreflang="fa" class="interlanguage-link-target">فارسی</a></li><li class="interlanguage-link interwiki-fi"><a href="https://fi.wikipedia.org/wiki/Pii_(vakio)" title="Pii (vakio) – 핀란드어" lang="fi" hreflang="fi" class="interlanguage-link-target">Suomi</a></li><li class="interlanguage-link interwiki-fur"><a href="https://fur.wikipedia.org/wiki/Pi_gr%C3%AAc" title="Pi grêc – 프리울리어" lang="fur" hreflang="fur" class="interlanguage-link-target">Furlan</a></li><li class="interlanguage-link interwiki-ga"><a href="https://ga.wikipedia.org/wiki/Pi" title="Pi – 아일랜드어" lang="ga" hreflang="ga" class="interlanguage-link-target">Gaeilge</a></li><li class="interlanguage-link interwiki-gan"><a href="https://gan.wikipedia.org/wiki/%E5%9C%93%E5%91%A8%E7%8E%87" title="圓周率 – 간어" lang="gan" hreflang="gan" class="interlanguage-link-target">贛語</a></li><li class="interlanguage-link interwiki-gl"><a href="https://gl.wikipedia.org/wiki/N%C3%BAmero_pi" title="Número pi – 갈리시아어" lang="gl" hreflang="gl" class="interlanguage-link-target">Galego</a></li><li class="interlanguage-link interwiki-haw"><a href="https://haw.wikipedia.org/wiki/Pai_(makemakika)" title="Pai (makemakika) – 하와이어" lang="haw" hreflang="haw" class="interlanguage-link-target">Hawaiʻi</a></li><li class="interlanguage-link interwiki-he"><a href="https://he.wikipedia.org/wiki/%D7%A4%D7%90%D7%99" title="פאי – 히브리어" lang="he" hreflang="he" class="interlanguage-link-target">עברית</a></li><li class="interlanguage-link interwiki-hi"><a href="https://hi.wikipedia.org/wiki/%E0%A4%AA%E0%A4%BE%E0%A4%88" title="पाई – 힌디어" lang="hi" hreflang="hi" class="interlanguage-link-target">हिन्दी</a></li><li class="interlanguage-link interwiki-hr"><a href="https://hr.wikipedia.org/wiki/Pi_(broj)" title="Pi (broj) – 크로아티아어" lang="hr" hreflang="hr" class="interlanguage-link-target">Hrvatski</a></li><li class="interlanguage-link interwiki-hsb"><a href="https://hsb.wikipedia.org/wiki/Konstanta_%CF%80" title="Konstanta π – 고지 소르비아어" lang="hsb" hreflang="hsb" class="interlanguage-link-target">Hornjoserbsce</a></li><li class="interlanguage-link interwiki-ht"><a href="https://ht.wikipedia.org/wiki/Pi_(matematik)" title="Pi (matematik) – 아이티어" lang="ht" hreflang="ht" class="interlanguage-link-target">Kreyòl ayisyen</a></li><li class="interlanguage-link interwiki-hy"><a href="https://hy.wikipedia.org/wiki/%D5%8A%D5%AB_%D5%A9%D5%AB%D5%BE" title="Պի թիվ – 아르메니아어" lang="hy" hreflang="hy" class="interlanguage-link-target">Հայերեն</a></li><li class="interlanguage-link interwiki-ia"><a href="https://ia.wikipedia.org/wiki/Pi" title="Pi – 인터링구아" lang="ia" hreflang="ia" class="interlanguage-link-target">Interlingua</a></li><li class="interlanguage-link interwiki-id"><a href="https://id.wikipedia.org/wiki/Pi" title="Pi – 인도네시아어" lang="id" hreflang="id" class="interlanguage-link-target">Bahasa Indonesia</a></li><li class="interlanguage-link interwiki-io"><a href="https://io.wikipedia.org/wiki/Pi" title="Pi – 이도어" lang="io" hreflang="io" class="interlanguage-link-target">Ido</a></li><li class="interlanguage-link interwiki-is"><a href="https://is.wikipedia.org/wiki/P%C3%AD" title="Pí – 아이슬란드어" lang="is" hreflang="is" class="interlanguage-link-target">Íslenska</a></li><li class="interlanguage-link interwiki-ja"><a href="https://ja.wikipedia.org/wiki/%E5%86%86%E5%91%A8%E7%8E%87" title="円周率 – 일본어" lang="ja" hreflang="ja" class="interlanguage-link-target">日本語</a></li><li class="interlanguage-link interwiki-jv"><a href="https://jv.wikipedia.org/wiki/Pi" title="Pi – 자바어" lang="jv" hreflang="jv" class="interlanguage-link-target">Jawa</a></li><li class="interlanguage-link interwiki-ka"><a href="https://ka.wikipedia.org/wiki/%E1%83%9E%E1%83%98_(%E1%83%A0%E1%83%98%E1%83%AA%E1%83%AE%E1%83%95%E1%83%98)" title="პი (რიცხვი) – 조지아어" lang="ka" hreflang="ka" class="interlanguage-link-target">ქართული</a></li><li class="interlanguage-link interwiki-kk"><a href="https://kk.wikipedia.org/wiki/%D0%9F%D0%B8_(%D1%81%D0%B0%D0%BD)" title="Пи (сан) – 카자흐어" lang="kk" hreflang="kk" class="interlanguage-link-target">Қазақша</a></li><li class="interlanguage-link interwiki-kn"><a href="https://kn.wikipedia.org/wiki/%E0%B2%AA%E0%B3%88" title="ಪೈ – 칸나다어" lang="kn" hreflang="kn" class="interlanguage-link-target">ಕನ್ನಡ</a></li><li class="interlanguage-link interwiki-ksh"><a href="https://ksh.wikipedia.org/wiki/Pi_(Kr%C3%A4j%C3%9Fzal)" title="Pi (Kräjßzal) – 콜로그니안어" lang="ksh" hreflang="ksh" class="interlanguage-link-target">Ripoarisch</a></li><li class="interlanguage-link interwiki-ku"><a href="https://ku.wikipedia.org/wiki/Pi" title="Pi – 쿠르드어" lang="ku" hreflang="ku" class="interlanguage-link-target">Kurdî</a></li><li class="interlanguage-link interwiki-lb"><a href="https://lb.wikipedia.org/wiki/Pi_(Zuel)" title="Pi (Zuel) – 룩셈부르크어" lang="lb" hreflang="lb" class="interlanguage-link-target">Lëtzebuergesch</a></li><li class="interlanguage-link interwiki-li"><a href="https://li.wikipedia.org/wiki/Pi_(wisk%C3%B3nde)" title="Pi (wiskónde) – 림버거어" lang="li" hreflang="li" class="interlanguage-link-target">Limburgs</a></li><li class="interlanguage-link interwiki-lmo"><a href="https://lmo.wikipedia.org/wiki/N%C3%BCmar_Pi" title="Nümar Pi – Lombard" lang="lmo" hreflang="lmo" class="interlanguage-link-target">Lumbaart</a></li><li class="interlanguage-link interwiki-lt"><a href="https://lt.wikipedia.org/wiki/Pi" title="Pi – 리투아니아어" lang="lt" hreflang="lt" class="interlanguage-link-target">Lietuvių</a></li><li class="interlanguage-link interwiki-lv"><a href="https://lv.wikipedia.org/wiki/P%C4%AB" title="Pī – 라트비아어" lang="lv" hreflang="lv" class="interlanguage-link-target">Latviešu</a></li><li class="interlanguage-link interwiki-mg"><a href="https://mg.wikipedia.org/wiki/Pi" title="Pi – 말라가시어" lang="mg" hreflang="mg" class="interlanguage-link-target">Malagasy</a></li><li class="interlanguage-link interwiki-ml"><a href="https://ml.wikipedia.org/wiki/%E0%B4%AA%E0%B5%88_(%E0%B4%97%E0%B4%A3%E0%B4%BF%E0%B4%A4%E0%B4%82)" title="പൈ (ഗണിതം) – 말라얄람어" lang="ml" hreflang="ml" class="interlanguage-link-target">മലയാളം</a></li><li class="interlanguage-link interwiki-mn"><a href="https://mn.wikipedia.org/wiki/%D0%9F%D0%B8" title="Пи – 몽골어" lang="mn" hreflang="mn" class="interlanguage-link-target">Монгол</a></li><li class="interlanguage-link interwiki-ms"><a href="https://ms.wikipedia.org/wiki/Pi" title="Pi – 말레이어" lang="ms" hreflang="ms" class="interlanguage-link-target">Bahasa Melayu</a></li><li class="interlanguage-link interwiki-my"><a href="https://my.wikipedia.org/wiki/%E1%80%95%E1%80%AD%E1%80%AF%E1%80%84%E1%80%BA" title="ပိုင် – 버마어" lang="my" hreflang="my" class="interlanguage-link-target">မြန်မာဘာသာ</a></li><li class="interlanguage-link interwiki-nds"><a href="https://nds.wikipedia.org/wiki/Krinktall" title="Krinktall – 저지 독일어" lang="nds" hreflang="nds" class="interlanguage-link-target">Plattdüütsch</a></li><li class="interlanguage-link interwiki-new"><a href="https://new.wikipedia.org/wiki/%E0%A4%AA%E0%A4%BE%E0%A4%87" title="पाइ – 네와르어" lang="new" hreflang="new" class="interlanguage-link-target">नेपाल भाषा</a></li><li class="interlanguage-link interwiki-nn"><a href="https://nn.wikipedia.org/wiki/Pi" title="Pi – 노르웨이어(니노르스크)" lang="nn" hreflang="nn" class="interlanguage-link-target">Norsk nynorsk</a></li><li class="interlanguage-link interwiki-no"><a href="https://no.wikipedia.org/wiki/Pi" title="Pi – 노르웨이어(보크말)" lang="nb" hreflang="nb" class="interlanguage-link-target">Norsk bokmål</a></li><li class="interlanguage-link interwiki-oc"><a href="https://oc.wikipedia.org/wiki/Pi" title="Pi – 오크어" lang="oc" hreflang="oc" class="interlanguage-link-target">Occitan</a></li><li class="interlanguage-link interwiki-os"><a href="https://os.wikipedia.org/wiki/%D0%9F%D0%B8" title="Пи – 오세트어" lang="os" hreflang="os" class="interlanguage-link-target">Ирон</a></li><li class="interlanguage-link interwiki-pcd"><a href="https://pcd.wikipedia.org/wiki/Pi" title="Pi – Picard" lang="pcd" hreflang="pcd" class="interlanguage-link-target">Picard</a></li><li class="interlanguage-link interwiki-pl"><a href="https://pl.wikipedia.org/wiki/Pi" title="Pi – 폴란드어" lang="pl" hreflang="pl" class="interlanguage-link-target">Polski</a></li><li class="interlanguage-link interwiki-pms"><a href="https://pms.wikipedia.org/wiki/N%C3%B9mer_%C3%ABd_Ludolph" title="Nùmer ëd Ludolph – Piedmontese" lang="pms" hreflang="pms" class="interlanguage-link-target">Piemontèis</a></li><li class="interlanguage-link interwiki-pnb"><a href="https://pnb.wikipedia.org/wiki/%D9%BE%D8%A7%D8%A6%DB%8C" title="پائی – Western Punjabi" lang="pnb" hreflang="pnb" class="interlanguage-link-target">پنجابی</a></li><li class="interlanguage-link interwiki-qu"><a href="https://qu.wikipedia.org/wiki/Chiqaluwa" title="Chiqaluwa – 케추아어" lang="qu" hreflang="qu" class="interlanguage-link-target">Runa Simi</a></li><li class="interlanguage-link interwiki-ru"><a href="https://ru.wikipedia.org/wiki/%D0%9F%D0%B8_(%D1%87%D0%B8%D1%81%D0%BB%D0%BE)" title="Пи (число) – 러시아어" lang="ru" hreflang="ru" class="interlanguage-link-target">Русский</a></li><li class="interlanguage-link interwiki-rue"><a href="https://rue.wikipedia.org/wiki/%D0%A7%D1%96%D1%81%D0%BB%D0%BE_%D0%BF%D1%96" title="Чісло пі – 루신어" lang="rue" hreflang="rue" class="interlanguage-link-target">Русиньскый</a></li><li class="interlanguage-link interwiki-sah"><a href="https://sah.wikipedia.org/wiki/%D0%9F%D0%B8" title="Пи – 야쿠트어" lang="sah" hreflang="sah" class="interlanguage-link-target">Саха тыла</a></li><li class="interlanguage-link interwiki-scn"><a href="https://scn.wikipedia.org/wiki/Pi_grecu" title="Pi grecu – 시칠리아어" lang="scn" hreflang="scn" class="interlanguage-link-target">Sicilianu</a></li><li class="interlanguage-link interwiki-sco"><a href="https://sco.wikipedia.org/wiki/Pi" title="Pi – 스코틀랜드어" lang="sco" hreflang="sco" class="interlanguage-link-target">Scots</a></li><li class="interlanguage-link interwiki-sh"><a href="https://sh.wikipedia.org/wiki/Pi" title="Pi – 세르비아-크로아티아어" lang="sh" hreflang="sh" class="interlanguage-link-target">Srpskohrvatski / српскохрватски</a></li><li class="interlanguage-link interwiki-si"><a href="https://si.wikipedia.org/wiki/%E0%B6%B4%E0%B6%BA%E0%B7%92_(%E0%B6%85%E0%B6%82%E0%B6%9A%E0%B6%BA)" title="පයි (අංකය) – 스리랑카어" lang="si" hreflang="si" class="interlanguage-link-target">සිංහල</a></li><li class="interlanguage-link interwiki-simple"><a href="https://simple.wikipedia.org/wiki/Pi" title="Pi – Simple English" lang="en-simple" hreflang="en-simple" class="interlanguage-link-target">Simple English</a></li><li class="interlanguage-link interwiki-sk"><a href="https://sk.wikipedia.org/wiki/Ludolfovo_%C4%8D%C3%ADslo" title="Ludolfovo číslo – 슬로바키아어" lang="sk" hreflang="sk" class="interlanguage-link-target">Slovenčina</a></li><li class="interlanguage-link interwiki-sl"><a href="https://sl.wikipedia.org/wiki/Pi" title="Pi – 슬로베니아어" lang="sl" hreflang="sl" class="interlanguage-link-target">Slovenščina</a></li><li class="interlanguage-link interwiki-sq"><a href="https://sq.wikipedia.org/wiki/Numri_pi" title="Numri pi – 알바니아어" lang="sq" hreflang="sq" class="interlanguage-link-target">Shqip</a></li><li class="interlanguage-link interwiki-sr"><a href="https://sr.wikipedia.org/wiki/%D0%9F%D0%B8" title="Пи – 세르비아어" lang="sr" hreflang="sr" class="interlanguage-link-target">Српски / srpski</a></li><li class="interlanguage-link interwiki-sv"><a href="https://sv.wikipedia.org/wiki/Pi" title="Pi – 스웨덴어" lang="sv" hreflang="sv" class="interlanguage-link-target">Svenska</a></li><li class="interlanguage-link interwiki-szl"><a href="https://szl.wikipedia.org/wiki/Pi" title="Pi – Silesian" lang="szl" hreflang="szl" class="interlanguage-link-target">Ślůnski</a></li><li class="interlanguage-link interwiki-ta"><a href="https://ta.wikipedia.org/wiki/%E0%AE%AA%E0%AF%88_(%E0%AE%95%E0%AE%A3%E0%AE%BF%E0%AE%A4_%E0%AE%AE%E0%AE%BE%E0%AE%B1%E0%AE%BF%E0%AE%B2%E0%AE%BF)" title="பை (கணித மாறிலி) – 타밀어" lang="ta" hreflang="ta" class="interlanguage-link-target">தமிழ்</a></li><li class="interlanguage-link interwiki-te"><a href="https://te.wikipedia.org/wiki/%E0%B0%AA%E0%B1%88" title="పై – 텔루구어" lang="te" hreflang="te" class="interlanguage-link-target">తెలుగు</a></li><li class="interlanguage-link interwiki-th"><a href="https://th.wikipedia.org/wiki/%E0%B8%9E%E0%B8%B2%E0%B8%A2_(%E0%B8%84%E0%B9%88%E0%B8%B2%E0%B8%84%E0%B8%87%E0%B8%95%E0%B8%B1%E0%B8%A7)" title="พาย (ค่าคงตัว) – 태국어" lang="th" hreflang="th" class="interlanguage-link-target">ไทย</a></li><li class="interlanguage-link interwiki-tl"><a href="https://tl.wikipedia.org/wiki/Pi" title="Pi – 타갈로그어" lang="tl" hreflang="tl" class="interlanguage-link-target">Tagalog</a></li><li class="interlanguage-link interwiki-tr"><a href="https://tr.wikipedia.org/wiki/Pi_say%C4%B1s%C4%B1" title="Pi sayısı – 터키어" lang="tr" hreflang="tr" class="interlanguage-link-target">Türkçe</a></li><li class="interlanguage-link interwiki-tt"><a href="https://tt.wikipedia.org/wiki/%D0%9F%D0%B8_%D1%81%D0%B0%D0%BD%D1%8B" title="Пи саны – 타타르어" lang="tt" hreflang="tt" class="interlanguage-link-target">Татарча/tatarça</a></li><li class="interlanguage-link interwiki-uk"><a href="https://uk.wikipedia.org/wiki/%D0%A7%D0%B8%D1%81%D0%BB%D0%BE_%D0%BF%D1%96" title="Число пі – 우크라이나어" lang="uk" hreflang="uk" class="interlanguage-link-target">Українська</a></li><li class="interlanguage-link interwiki-ur"><a href="https://ur.wikipedia.org/wiki/%D9%BE%D8%A7%D8%A6%DB%8C" title="پائی – 우르두어" lang="ur" hreflang="ur" class="interlanguage-link-target">اردو</a></li><li class="interlanguage-link interwiki-uz"><a href="https://uz.wikipedia.org/wiki/Pi" title="Pi – 우즈베크어" lang="uz" hreflang="uz" class="interlanguage-link-target">Oʻzbekcha/ўзбекча</a></li><li class="interlanguage-link interwiki-vec"><a href="https://vec.wikipedia.org/wiki/Pi_greco" title="Pi greco – Venetian" lang="vec" hreflang="vec" class="interlanguage-link-target">Vèneto</a></li><li class="interlanguage-link interwiki-war"><a href="https://war.wikipedia.org/wiki/Pi" title="Pi – 와라이어" lang="war" hreflang="war" class="interlanguage-link-target">Winaray</a></li><li class="interlanguage-link interwiki-xal"><a href="https://xal.wikipedia.org/wiki/%D0%9F%D0%B8" title="Пи – 칼미크어" lang="xal" hreflang="xal" class="interlanguage-link-target">Хальмг</a></li><li class="interlanguage-link interwiki-yi"><a href="https://yi.wikipedia.org/wiki/%D7%A4%D7%99" title="פי – 이디시어" lang="yi" hreflang="yi" class="interlanguage-link-target">ייִדיש</a></li><li class="interlanguage-link interwiki-yo"><a href="https://yo.wikipedia.org/wiki/Pi" title="Pi – 요루바어" lang="yo" hreflang="yo" class="interlanguage-link-target">Yorùbá</a></li><li class="interlanguage-link interwiki-bat-smg"><a href="https://bat-smg.wikipedia.org/wiki/Pi" title="Pi – Samogitian" lang="sgs" hreflang="sgs" class="interlanguage-link-target">Žemaitėška</a></li><li class="interlanguage-link interwiki-roa-tara"><a href="https://roa-tara.wikipedia.org/wiki/Pi_greche" title="Pi greche – Tarantino" lang="nap-x-tara" hreflang="nap-x-tara" class="interlanguage-link-target">Tarandíne</a></li><li class="interlanguage-link interwiki-zh-classical"><a href="https://zh-classical.wikipedia.org/wiki/%E5%9C%93%E5%91%A8%E7%8E%87" title="圓周率 – Classical Chinese" lang="lzh" hreflang="lzh" class="interlanguage-link-target">文言</a></li><li class="interlanguage-link interwiki-zh-min-nan"><a href="https://zh-min-nan.wikipedia.org/wiki/%C3%8E%E2%81%BF-chiu-lu%CC%8Dt" title="Îⁿ-chiu-lu̍t – Chinese (Min Nan)" lang="nan" hreflang="nan" class="interlanguage-link-target">Bân-lâm-gú</a></li><li class="interlanguage-link interwiki-zh-yue"><a href="https://zh-yue.wikipedia.org/wiki/%E5%9C%93%E5%91%A8%E7%8E%87" title="圓周率 – Cantonese" lang="yue" hreflang="yue" class="interlanguage-link-target">粵語</a></li><li class="interlanguage-link interwiki-be-x-old"><a href="https://be-tarask.wikipedia.org/wiki/%D0%9F%D1%96" title="Пі – Belarusian (Taraškievica orthography)" lang="be-tarask" hreflang="be-tarask" class="interlanguage-link-target">Беларуская (тарашкевіца)</a></li><li class="interlanguage-link interwiki-ar"><a href="https://ar.wikipedia.org/wiki/%D8%B7_(%D8%B1%D9%8A%D8%A7%D8%B6%D9%8A%D8%A7%D8%AA)" title="ط (رياضيات) – 아랍어" lang="ar" hreflang="ar" class="interlanguage-link-target">العربية</a></li><li class="interlanguage-link interwiki-zea"><a href="https://zea.wikipedia.org/wiki/Pi_(wiskunde)" title="Pi (wiskunde) – Zeelandic" lang="zea" hreflang="zea" class="interlanguage-link-target">Zeêuws</a></li><li class="interlanguage-link interwiki-lez"><a href="https://lez.wikipedia.org/wiki/%D0%9F%D0%B8_(%D1%87%D0%B8%D1%81%D0%BB%D0%BE)" title="Пи (число) – 레즈기안어" lang="lez" hreflang="lez" class="interlanguage-link-target">Лезги</a></li><li class="interlanguage-link interwiki-fy"><a href="https://fy.wikipedia.org/wiki/Py_(wiskunde)" title="Py (wiskunde) – 서부 프리지아어" lang="fy" hreflang="fy" class="interlanguage-link-target">Frysk</a></li><li class="interlanguage-link interwiki-or"><a href="https://or.wikipedia.org/wiki/%E0%AC%AA%E0%AC%BE%E0%AC%87" title="ପାଇ – 오리야어" lang="or" hreflang="or" class="interlanguage-link-target">ଓଡ଼ିଆ</a></li><li class="interlanguage-link interwiki-sw"><a href="https://sw.wikipedia.org/wiki/Pi_(namba)" title="Pi (namba) – 스와힐리어" lang="sw" hreflang="sw" class="interlanguage-link-target">Kiswahili</a></li><li class="interlanguage-link interwiki-wuu"><a href="https://wuu.wikipedia.org/wiki/%E5%9C%93%E5%91%A8%E7%8E%87" title="圓周率 – 우어" lang="wuu" hreflang="wuu" class="interlanguage-link-target">吴语</a></li><li class="interlanguage-link interwiki-af badge-Q17437796 badge-featuredarticle" title="알찬 글"><a href="https://af.wikipedia.org/wiki/Pi" title="Pi – 아프리칸스어" lang="af" hreflang="af" class="interlanguage-link-target">Afrikaans</a></li><li class="interlanguage-link interwiki-ca badge-Q17437796 badge-featuredarticle" title="알찬 글"><a href="https://ca.wikipedia.org/wiki/Nombre_%CF%80" title="Nombre π – 카탈로니아어" lang="ca" hreflang="ca" class="interlanguage-link-target">Català</a></li><li class="interlanguage-link interwiki-de badge-Q17437796 badge-featuredarticle" title="알찬 글"><a href="https://de.wikipedia.org/wiki/Kreiszahl" title="Kreiszahl – 독일어" lang="de" hreflang="de" class="interlanguage-link-target">Deutsch</a></li><li class="interlanguage-link interwiki-eo badge-Q17437796 badge-featuredarticle" title="알찬 글"><a href="https://eo.wikipedia.org/wiki/Pi_(nombro)" title="Pi (nombro) – 에스페란토어" lang="eo" hreflang="eo" class="interlanguage-link-target">Esperanto</a></li><li class="interlanguage-link interwiki-mk badge-Q17437796 badge-featuredarticle" title="알찬 글"><a href="https://mk.wikipedia.org/wiki/%D0%9F%D0%B8" title="Пи – 마케도니아어" lang="mk" hreflang="mk" class="interlanguage-link-target">Македонски</a></li><li class="interlanguage-link interwiki-ro badge-Q17437796 badge-featuredarticle" title="알찬 글"><a href="https://ro.wikipedia.org/wiki/Pi" title="Pi – 루마니아어" lang="ro" hreflang="ro" class="interlanguage-link-target">Română</a></li><li class="interlanguage-link interwiki-vi badge-Q17437796 badge-featuredarticle" title="알찬 글"><a href="https://vi.wikipedia.org/wiki/Pi" title="Pi – 베트남어" lang="vi" hreflang="vi" class="interlanguage-link-target">Tiếng Việt</a></li><li class="interlanguage-link interwiki-pa"><a href="https://pa.wikipedia.org/wiki/%E0%A8%AA%E0%A8%BE%E0%A8%88" title="ਪਾਈ – 펀잡어" lang="pa" hreflang="pa" class="interlanguage-link-target">ਪੰਜਾਬੀ</a></li><li class="interlanguage-link interwiki-eml"><a href="https://eml.wikipedia.org/wiki/Pi_gr%C4%93c" title="Pi grēc – Emiliano-Romagnolo" lang="egl" hreflang="egl" class="interlanguage-link-target">Emiliàn e rumagnòl</a></li><li class="interlanguage-link interwiki-bxr"><a href="https://bxr.wikipedia.org/wiki/%D0%9F%D0%B8_(%D1%82%D0%BE%D0%BE)" title="Пи (тоо) – Russia Buriat" lang="bxr" hreflang="bxr" class="interlanguage-link-target">Буряад</a></li><li class="interlanguage-link interwiki-ckb"><a href="https://ckb.wikipedia.org/wiki/%D9%BE%D8%A7%DB%8C" title="پای – 소라니 쿠르드어" lang="ckb" hreflang="ckb" class="interlanguage-link-target">کوردی</a></li><li class="interlanguage-link interwiki-so"><a href="https://so.wikipedia.org/wiki/Summad_(Pi)" title="Summad (Pi) – 소말리아어" lang="so" hreflang="so" class="interlanguage-link-target">Soomaaliga</a></li><li class="interlanguage-link interwiki-sc"><a href="https://sc.wikipedia.org/wiki/Pi_grecu" title="Pi grecu – 사르디니아어" lang="sc" hreflang="sc" class="interlanguage-link-target">Sardu</a></li><li class="interlanguage-link interwiki-el"><a href="https://el.wikipedia.org/wiki/%CE%A0_(%CE%BC%CE%B1%CE%B8%CE%B7%CE%BC%CE%B1%CF%84%CE%B9%CE%BA%CE%AE_%CF%83%CF%84%CE%B1%CE%B8%CE%B5%CF%81%CE%AC)" title="Π (μαθηματική σταθερά) – 그리스어" lang="el" hreflang="el" class="interlanguage-link-target">Ελληνικά</a></li><li class="interlanguage-link interwiki-arz"><a href="https://arz.wikipedia.org/wiki/%D8%A8%D8%A7%D9%89_(%D8%B1%D9%8A%D8%A7%D8%B6%D9%8A%D8%A7%D8%AA)" title="باى (رياضيات) – 이집트 아랍어" lang="arz" hreflang="arz" class="interlanguage-link-target">مصرى</a></li><li class="interlanguage-link interwiki-gu"><a href="https://gu.wikipedia.org/wiki/%E0%AA%AA%E0%AA%BE%E0%AA%87" title="પાઇ – 구자라트어" lang="gu" hreflang="gu" class="interlanguage-link-target">ગુજરાતી</a></li><li class="interlanguage-link interwiki-azb"><a href="https://azb.wikipedia.org/wiki/%D9%BE%DB%8C_%D8%B3%D8%A7%DB%8C%DB%8C%E2%80%8C%D8%B3%DB%8C" title="پی ساییسی – South Azerbaijani" lang="azb" hreflang="azb" class="interlanguage-link-target">تۆرکجه</a></li><li class="interlanguage-link interwiki-cy"><a href="https://cy.wikipedia.org/wiki/Pi_(mathemateg)" title="Pi (mathemateg) – 웨일스어" lang="cy" hreflang="cy" class="interlanguage-link-target">Cymraeg</a></li><li class="interlanguage-link interwiki-jam"><a href="https://jam.wikipedia.org/wiki/Pi" title="Pi – Jamaican Creole English" lang="jam" hreflang="jam" class="interlanguage-link-target">Patois</a></li><li class="interlanguage-link interwiki-hu"><a href="https://hu.wikipedia.org/wiki/P%C3%AD_(sz%C3%A1m)" title="Pí (szám) – 헝가리어" lang="hu" hreflang="hu" class="interlanguage-link-target">Magyar</a></li><li class="interlanguage-link interwiki-fj"><a href="https://fj.wikipedia.org/wiki/Pi" title="Pi – 피지어" lang="fj" hreflang="fj" class="interlanguage-link-target">Na Vosa Vakaviti</a></li><li class="interlanguage-link interwiki-la badge-Q17437796 badge-featuredarticle" title="알찬 글"><a href="https://la.wikipedia.org/wiki/Numerus_pi" title="Numerus pi – 라틴어" lang="la" hreflang="la" class="interlanguage-link-target">Latina</a></li><li class="interlanguage-link interwiki-cdo"><a href="https://cdo.wikipedia.org/wiki/I%C3%A8ng-ci%C5%AD-l%E1%B9%B3%CC%86k" title="Ièng-ciŭ-lṳ̆k – Min Dong Chinese" lang="cdo" hreflang="cdo" class="interlanguage-link-target">Mìng-dĕ̤ng-ngṳ̄</a></li><li class="interlanguage-link interwiki-fo"><a href="https://fo.wikipedia.org/wiki/Pi" title="Pi – 페로어" lang="fo" hreflang="fo" class="interlanguage-link-target">Føroyskt</a></li><li class="interlanguage-link interwiki-br"><a href="https://br.wikipedia.org/wiki/Pi_(niver)" title="Pi (niver) – 브르타뉴어" lang="br" hreflang="br" class="interlanguage-link-target">Brezhoneg</a></li><li class="interlanguage-link interwiki-es"><a href="https://es.wikipedia.org/wiki/N%C3%BAmero_%CF%80" title="Número π – 스페인어" lang="es" hreflang="es" class="interlanguage-link-target">Español</a></li><li class="interlanguage-link interwiki-ky"><a href="https://ky.wikipedia.org/wiki/%D0%9F%D0%B8" title="Пи – 키르기스어" lang="ky" hreflang="ky" class="interlanguage-link-target">Кыргызча</a></li><li class="interlanguage-link interwiki-sat"><a href="https://sat.wikipedia.org/wiki/%E1%B1%AF%E1%B1%9F%E1%B1%AD" title="ᱯᱟᱭ – 산탈리어" lang="sat" hreflang="sat" class="interlanguage-link-target">ᱥᱟᱱᱛᱟᱲᱤ</a></li><li class="interlanguage-link interwiki-pfl"><a href="https://pfl.wikipedia.org/wiki/Kreiszahl" title="Kreiszahl – Palatine German" lang="pfl" hreflang="pfl" class="interlanguage-link-target">Pälzisch</a></li><li class="interlanguage-link interwiki-zh badge-Q17437798 badge-goodarticle" title="좋은 글"><a href="https://zh.wikipedia.org/wiki/%E5%9C%93%E5%91%A8%E7%8E%87" title="圓周率 – 중국어" lang="zh" hreflang="zh" class="interlanguage-link-target">中文</a></li><li class="interlanguage-link interwiki-ast"><a href="https://ast.wikipedia.org/wiki/N%C3%BAmberu_%CF%80" title="Númberu π – 아스투리아어" lang="ast" hreflang="ast" class="interlanguage-link-target">Asturianu</a></li><li class="interlanguage-link interwiki-cs badge-Q17437798 badge-goodarticle" title="좋은 글"><a href="https://cs.wikipedia.org/wiki/P%C3%AD_(%C4%8D%C3%ADslo)" title="Pí (číslo) – 체코어" lang="cs" hreflang="cs" class="interlanguage-link-target">Čeština</a></li><li class="interlanguage-link interwiki-ne"><a href="https://ne.wikipedia.org/wiki/%E0%A4%AA%E0%A4%BE%E0%A4%88" title="पाई – 네팔어" lang="ne" hreflang="ne" class="interlanguage-link-target">नेपाली</a></li><li class="interlanguage-link interwiki-en badge-Q17437796 badge-featuredarticle" title="알찬 글"><a href="https://en.wikipedia.org/wiki/Pi" title="Pi – 영어" lang="en" hreflang="en" class="interlanguage-link-target">English</a></li><li class="interlanguage-link interwiki-cv"><a href="https://cv.wikipedia.org/wiki/%D0%9F%D0%B8_(%D1%85%D0%B8%D1%81%D0%B5%D0%BF)" title="Пи (хисеп) – 추바시어" lang="cv" hreflang="cv" class="interlanguage-link-target">Чӑвашла</a></li><li class="interlanguage-link interwiki-mr"><a href="https://mr.wikipedia.org/wiki/%E0%A4%AA%E0%A4%BE%E0%A4%AF_(%E0%A4%B8%E0%A5%8D%E0%A4%A5%E0%A4%BF%E0%A4%B0%E0%A4%BE%E0%A4%82%E0%A4%95)" title="पाय (स्थिरांक) – 마라티어" lang="mr" hreflang="mr" class="interlanguage-link-target">मराठी</a></li><li class="interlanguage-link interwiki-nl"><a href="https://nl.wikipedia.org/wiki/Pi_(wiskunde)" title="Pi (wiskunde) – 네덜란드어" lang="nl" hreflang="nl" class="interlanguage-link-target">Nederlands</a></li><li class="interlanguage-link interwiki-gcr"><a href="https://gcr.wikipedia.org/wiki/Pi" title="Pi – Guianan Creole" lang="gcr" hreflang="gcr" class="interlanguage-link-target">Kriyòl gwiyannen</a></li><li class="interlanguage-link interwiki-ba"><a href="https://ba.wikipedia.org/wiki/%D0%9F%D0%B8_(%D2%BB%D0%B0%D0%BD)" title="Пи (һан) – 바슈키르어" lang="ba" hreflang="ba" class="interlanguage-link-target">Башҡортса</a></li><li class="interlanguage-link interwiki-kw"><a href="https://kw.wikipedia.org/wiki/Pi" title="Pi – 콘월어" lang="kw" hreflang="kw" class="interlanguage-link-target">Kernowek</a></li><li class="interlanguage-link interwiki-gd"><a href="https://gd.wikipedia.org/wiki/Pi_(%C3%A0ireamh)" title="Pi (àireamh) – 스코틀랜드 게일어" lang="gd" hreflang="gd" class="interlanguage-link-target">Gàidhlig</a></li></ul>
<div class="after-portlet after-portlet-lang"><span class="wb-langlinks-edit wb-langlinks-link"><a href="https://www.wikidata.org/wiki/Special:EntityPage/Q167#sitelinks-wikipedia" title="언어 인터위키 링크 편집" class="wbc-editpage">링크 편집</a></span></div>
</div>
</nav>
</div>
</div>
<footer id="footer" class="mw-footer" role="contentinfo" >
<ul id="footer-info" >
<li id="footer-info-lastmod"> 이 문서는 2020년 7월 8일 (수) 15:55에 마지막으로 편집되었습니다.</li>
<li id="footer-info-copyright">모든 문서는 <a href="//ko.wikipedia.org/wiki/%EC%9C%84%ED%82%A4%EB%B0%B1%EA%B3%BC:Creative_Commons_Attribution-ShareAlike_3.0_Unported_License">크리에이티브 커먼즈 저작자표시-동일조건변경허락 3.0</a>에 따라 사용할 수 있으며, 추가적인 조건이 적용될 수 있습니다. 자세한 내용은 <a href="//wikimediafoundation.org/wiki/Terms_of_Use/ko">이용 약관</a>을 참고하십시오.<br />Wikipedia®는 미국 및 다른 국가에 등록되어 있는 <a class='internal' href="http://www.wikimediafoundation.org">Wikimedia Foundation, Inc.</a> 소유의 등록 상표입니다.</li>
</ul>
<ul id="footer-places" >
<li id="footer-places-privacy"><a href="https://foundation.wikimedia.org/wiki/Privacy_policy" class="extiw" title="wmf:Privacy policy">개인정보처리방침</a></li>
<li id="footer-places-about"><a href="/wiki/%EC%9C%84%ED%82%A4%EB%B0%B1%EA%B3%BC:%EC%86%8C%EA%B0%9C" title="위키백과:소개">위키백과 소개</a></li>
<li id="footer-places-disclaimer"><a href="/wiki/%EC%9C%84%ED%82%A4%EB%B0%B1%EA%B3%BC:%EB%A9%B4%EC%B1%85_%EC%A1%B0%ED%95%AD" title="위키백과:면책 조항">면책 조항</a></li>
<li id="footer-places-developers"><a href="https://www.mediawiki.org/wiki/Special:MyLanguage/How_to_contribute">개발자</a></li>
<li id="footer-places-statslink"><a href="https://stats.wikimedia.org/#/ko.wikipedia.org">통계</a></li>
<li id="footer-places-cookiestatement"><a href="https://foundation.wikimedia.org/wiki/Cookie_statement">쿠키 정책</a></li>
<li id="footer-places-mobileview"><a href="//ko.m.wikipedia.org/w/index.php?title=%EC%9B%90%EC%A3%BC%EC%9C%A8&mobileaction=toggle_view_mobile" class="noprint stopMobileRedirectToggle">모바일 보기</a></li>
</ul>
<ul id="footer-icons" class="noprint">
<li id="footer-copyrightico"><a href="https://wikimediafoundation.org/"><img src="/static/images/wikimedia-button.png" srcset="/static/images/wikimedia-button-1.5x.png 1.5x, /static/images/wikimedia-button-2x.png 2x" width="88" height="31" alt="Wikimedia Foundation" loading="lazy" /></a></li>
<li id="footer-poweredbyico"><a href="https://www.mediawiki.org/"><img src="/static/images/poweredby_mediawiki_88x31.png" alt="Powered by MediaWiki" srcset="/static/images/poweredby_mediawiki_132x47.png 1.5x, /static/images/poweredby_mediawiki_176x62.png 2x" width="88" height="31" loading="lazy"/></a></li>
</ul>
<div style="clear: both;"></div>
</footer>
<script>(RLQ=window.RLQ||[]).push(function(){mw.config.set({"wgPageParseReport":{"limitreport":{"cputime":"0.720","walltime":"1.038","ppvisitednodes":{"value":5673,"limit":1000000},"postexpandincludesize":{"value":73730,"limit":2097152},"templateargumentsize":{"value":4580,"limit":2097152},"expansiondepth":{"value":15,"limit":40},"expensivefunctioncount":{"value":3,"limit":500},"unstrip-depth":{"value":1,"limit":20},"unstrip-size":{"value":70361,"limit":5000000},"entityaccesscount":{"value":1,"limit":400},"timingprofile":["100.00% 680.733 1 -total"," 39.85% 271.282 1 틀:각주"," 20.92% 142.415 17 틀:ISBN"," 14.06% 95.703 1 틀:무리수"," 13.43% 91.438 2 틀:둘러보기_상자"," 11.64% 79.207 4 틀:서적_인용"," 10.67% 72.637 17 틀:Catalog_lookup_link"," 9.56% 65.064 1 틀:좋은_글"," 9.02% 61.395 1 틀:상단_아이콘"," 7.10% 48.316 1 틀:Category_handler"]},"scribunto":{"limitreport-timeusage":{"value":"0.164","limit":"10.000"},"limitreport-memusage":{"value":5204443,"limit":52428800}},"cachereport":{"origin":"mw1373","timestamp":"20200714210535","ttl":2592000,"transientcontent":false}}});});</script>
<script type="application/ld+json">{"@context":"https:\/\/schema.org","@type":"Article","name":"\uc6d0\uc8fc\uc728","url":"https:\/\/ko.wikipedia.org\/wiki\/%EC%9B%90%EC%A3%BC%EC%9C%A8","sameAs":"http:\/\/www.wikidata.org\/entity\/Q167","mainEntity":"http:\/\/www.wikidata.org\/entity\/Q167","author":{"@type":"Organization","name":"\uc704\ud0a4\ubbf8\ub514\uc5b4 \ud504\ub85c\uc81d\ud2b8 \uae30\uc5ec\uc790"},"publisher":{"@type":"Organization","name":"Wikimedia Foundation, Inc.","logo":{"@type":"ImageObject","url":"https:\/\/www.wikimedia.org\/static\/images\/wmf-hor-googpub.png"}},"datePublished":"2003-08-04T19:18:08Z","dateModified":"2020-07-08T06:55:31Z","image":"https:\/\/upload.wikimedia.org\/wikipedia\/commons\/2\/2e\/Pi-symbol.svg","headline":"\uc6d0\uc758 \uc9c0\ub984\uacfc \ub458\ub808\uc758 \ube44"}</script>
<script>(RLQ=window.RLQ||[]).push(function(){mw.config.set({"wgBackendResponseTime":194,"wgHostname":"mw1270"});});</script></body></html>
Process finished with exit code 0
뭐 길다 잘 온다.
table 만 받아와 보자
import requests
from bs4 import BeautifulSoup
req = requests.get("https://ko.wikipedia.org/wiki/%EC%9B%90%EC%A3%BC%EC%9C%A8")
raw = req.text
html = BeautifulSoup(raw,"html.parser")
infos = html.select('table')
print(infos)
받아온 info 를 html preview 해보면

근데 생각해 보면 자바스크립트로 만들라고 하셨는데
크롤러가 아니라 파일 인풋받는거였는데
뭐한건지 ㄹㅡ겠다.
<!DOCTYPE html>
<html>
<head>
<meta charset="UTF-8">
<title>HTML 문서에서 테이블 추출</title>
<script type="text/javascript">
window.onload = function() {
//제출하기 clickListener
document.getElementById("submit").onclick = function() { // on click
loadFileAsText()
}
}
//HTML File -> show table
function loadFileAsText(){
var fileToLoad = document.getElementById("fileToLoad").files[0];
var fileReader = new FileReader();
fileReader.onload = function(fileLoadedEvent){
//불러온 텍스트 파일
var textFromFileLoaded = fileLoadedEvent.target.result;
//html 형식
var html = new DOMParser().parseFromString(textFromFileLoaded, "text/html");
//table 추출
var table = html.querySelector("table");
//원문 html 문자열
var htmlString = html.documentElement.outerHTML
//테이블 표시
document.getElementById("disp").appendChild(table);
//원문 표시
document.getElementById("html").innerHTML = htmlString
};
fileReader.readAsText(fileToLoad, "UTF-8");
}
</script>
</head>
<body>
<hr>
<input type="file" id="fileToLoad" accept="html/*" />
<button id="submit">제출하기</button>
<br>
<br>
<hr>
<div id="disp">표 출력</div>
<br>
<br>
<hr>
<div id="html">원문 출력</div>
</body>
</html>